1109145102

2.2 Drgania własne

Przechodzimy do badania równania opisującego drgania liniowego układu o jednym stopniu swobody. W przypadku wystąpienia tłumienia model Voigta opisany powyżej określa siłę kinetyczną działającą na układ jako cq -f kq. Równanie drgań swobodnych (bez działania siły zewnętrznej) jest wtedy opisane równaniem

mq + cq + kq — 0.    (54)

Przykładowo ruch masy skupionej m (ugięcie belki w środku przęsła, q) umieszczonej w środku rozpiętości belki swobodnie podpartej (Rys. 8) jest opisywany równaniem, w którym k — 48EI/l³. Współczynnik tłumienia musi być określony dodatkowo i do tego problemu powrócimy nieco później. Łatwo sprawdzić, że częstość drgań belki bez tłumienia wynosi u,i<jsk = 6,9282 ^/EI/ml³. Dla belki z ciągłym rozkładem masy otrzymuje sif Wcjąg = 7r²y/EI/ml³. Problem ten omawiamy w dalszej części kursu.

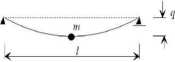
Rys. 8: Drgania swobodne belki z masą skupioną

Przystępujemy do rozwiązania równania (54). Jest to równanie liniowe o stałych współczynnikach. Szukamy więc rozwiązania o postaci q ~ e^rt. Podstawienie tej funkcji w (54) prowadzi do równania charakterystycznego

mr² + cr + k — 0.    (55)

Postać rozwiązań tego równania zależy od wartości wyróżnika A

A = c² - 4km — —4km (l — a²) , a    —j—,    (56)

ż v fcrn

gdzie liczbę a nazywamy liczbą tłumienia.

1. Dla liczby tłumienia a > 1 wyróżnik A jest dodatni i ogólne rozwiązanie problemu ma postać

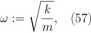
q = .Aexp w + Vc*² — lj t^ + Bexp y— w    — Vct² — lj tj ,

gdzie A, B są dowolnymi liczbami rzeczywistymi nierównymi równocześnie zero. Ponieważ \/a² — 1 < a więc dla dodatnich a oba wykładniki są ujemne. Oznacza to, że rozwiązanie q jest monotonicznie maleją funkcją czasu. Na skutek dużego tłumienia drgania nie wystąpią. Jest to tzw. tłumienie aperiodyczne, a ruch nazywa się ruchem pełzającym.

2. Dla liczby tłumienia a < 1 wyróżnik A jest ujemny i pierwiastki równania (55) mają postać

(58)

'1,2 = —au> ± iu>',

16