1109145110

- o nieskończonej liczbie stopni swobody (układy ciągłe).

Jest oczywiste, że w ramach opisu makroskopowego wszystkie układy powinny należeć do drugiej klasy. Jednakże w wielu praktycznie ważnych przypadkach przybliżenie układami, należącymi do pierwszej klasy jest wystarczające. Przekształcenie dynamicznego układu ciągłego do układu dyskretnego można otrzymać przez dyskretyzację ciągłego pola masowego przy pomocy granulacji mas - dyskretyzacja fizyczna, albo zamiany równań różniczkowych cząstkowych przez równania różniczkowe zwyczajne względem czasu - dyskretyzacja matematyczna.

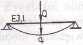
Jak już wspominaliśmy, więzi odkształcalne, na przykład pręty sprężyste, nie zmieniają dynamicznej liczby stopni swobody. Do ich opisu wprowadza się pojęcie sztywności. Sztywnością k izolowanej więzi liniowo sprężystej nazywa się stosunek uogólnionej siły czynnej Q do odpowiadającego jej uogólnionego przemieszczenia q (patrz Rys. 2). Odwrotność sztywności 8 = 1/k nazywa się podatnością. Zakładamy, że więzi sprężyste są sklero-nomiczne (tzn. niezależne od czasu).

ą - Ql³/3EJ 6 - l³/3E3 k -3EJ/1³

ą-OdABEJ <5 - l³A8E3

k - 48EJ /l³

ą-Ql/EA S*l/EA k-EA/l

Rys. 2: Sztywność i podatność więzi sprężystych

Dla układów o skończonej liczbie stopni swobody własności sprężyste opisują macierze podatności i sztywności. Ich konstrukcję pokazujemy na przykładzie belki swobodnie podpartej (Rys. 3).

W przedstwaionym przykładzie mamy zależności

(6)

91    — 8nQi + 8uQ2,

92    = 8₂iQi + 8₂₂Q₂,

lub w postaci macierzowej

q = fq.

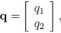
r ^121

[ ^21 822 \ ’

(7)

5