1060440355

a₂ .... a_k, których wartości należy określić. Zgodnie z ideą metody najmniejszych kwadratów, najlepszą ze wszystkich możliwych funkcji o założonej postaci będzie ta, dla której suma kwadratów odchyłek między' wartościami y, oraz obliczonymi y, = f( x,) dla / = 1 Nbędzie najmniejsza, czyli:

E(a_x,a₁....,a_k) = 'Y_J (y,-f(x,)) -►min    (4.3.1)

gdzie E jest wartością błędu aproksymacji.

Znalezienie wartości stałych ct\, a₂.... a_k sprowadza się do rozwiązania układu równań:

(4.3.2)

8E _ 8E _ 8E 8a_{ da₂    8a_k

czyli

f -i

^L=X 20, -f(x,))

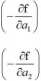
= 0 = 0

(4.3.3)

=Ż2fo-f«»    =0

Jest to układ k równań z k niewiadomymi, który ma jednoznaczne rozwiązanie ty lko w przypadku, gdy funkcja aproksymująca f(x) jest liniowo zależna od parametrów ct\, a₂ .... a_k co ma miejsce w przy padku funkcji wielomianowej. Dla układu równań nieliniowych rozwiązanie zagadnienia jest sprawą trudną, stąd aproksymację tą metodą stosuje się najczęściej do przypadków, w których funkcja aproksymująca jest liniowa lub można ją sprowadzić do postaci liniowej na drodze prostych przekształceń. Przy kładem może być funkcja postaci

f(x) = y=ax^h    (4.3.4)

którą można sprowadzić do postaci liniowej:

F(X) = Y = A+BX

stosując podstaw ienia: Zatem

Y = ln y; X = ln x; A = ln a: B = b

(4.3.5a) (4.3.5b)

(4.3.6)

(4.3.7)

Y_t = ln y_t oraz X_i = ln x,

oraz

E(A,B)=^ (Y_i -

Po obliczeniu pochodnych E względem A i B, przyrównaniu ich do zera i po rozwiązaniu układu równań liniowych (analogicznie do (4.3.3)) uzyskuje się:

12