1636661688

2. METODA SYMPLEKSOWA

19

Przypadek 2:

^cn ~ ^lN ^ 0. W szczególności niech dla pewnego indeksu j będzie cj — CgB^dj < 0 (stąd c^Tx < c^Tx).

Przypadek 2a:

Zakładamy, że B ¹a_J- < 0. Wówczas biorąc Vj =

—B~

gdzie ej jest

wektorem o n — m współrzędnych mającym jedynkę na miejscu j, a na pozostałych miejscach zero, otrzymujemy kierunkowy wektor ekstremalny. Wobec tego x = x + Vj, x £ X. Z równości c^Tx = c^Tx + c^TVj oraz c^Tx = c^Tx + (cjf — CqB~¹N)xn dostajemy

c^TVj = (c% — c^B ¹N)xn = cJ - CgB ^lcij < 0, czyli problem nie posiada rozwiązania.

Przypadek 2b:

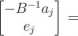
Zakładamy, że B~^ldj ^ 0. Weźmy Vj = | ^ ^aj'J i oznaczmy y = B~*dj, b = B~^lb. Niech A = mini<i<_m{|^; yi > 0} = x = x + AVj. Pokażemy, że x € X. Wiemy, że Ax = 6, natomiast Avj = [BN]vj = [i?iV]

—dj + dj = 0, zatem Ax = b. Musimy jeszcze udowodnić, że x > 0. Dla i = 1,2,..., m mamy

x = xi + A (vj)i = (B~^lb)i + — (—B~^ldj)i = h — —yt.

Uio    Vio

Rozważmy dwa przypadki:

1.    jeśli yi < 0, to oczywiście Xi > 0,

2.    jeśli yi > 0, to ^ a stąd Xi > 0.

Dla i = m + l,m + 2, ...,n oraz i ± j mamy Xi = 0. Dla i = j mamy Xi = A > 0. Wektor x posiada niezerowe współrzędne co najwyżej na miejscach 1,2,..., «o — 1, io+1, • • •, m,j- Pokażemy, że ai, a2,..., aj₀-i, di₀₊1,..., d_m, dj są liniowo niezależne. Wówczas x będzie punktem ekstremalnym. Załóżmy,