4544139883

2. Zmienne losowe 15

116.    Dobrać k tak, by funkcja

f 0    dla x < 0,

F(x) = { k arcsin® dla x G (0, 1],

[ 1    dla x > 1

była dystrybuantą pewnej zmiennej X, następnie wyznaczyć jej funkcję gęstości oraz obliczyć P{\ < X), P(X > 1), P(l < X < 1).

117.    Dobrać A i B tak, by funkcja

f 0    dla x < —1,

F(x) = \a + B arccosa: dla x € (—1, 1],

[ 1    dla x > 1

była dystrybuantą pewnej ciągłej zmiennej losowej X. Narysować wykres F, znaleźć funkcję gęstości, obliczyć P(0 < X < 1), P(X > |).

118.    Bok prostokąta jest zmienną losową X o rozkładzie jednostajnym na przedziale [0,10]. Obliczyć

a)    EX²,

b)    wartość oczekiwaną poła prostokąta, jeśli jego obwód wynosi 20.

119.    Zmienna X ma gęstość postaci

/(i) =

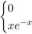
dla x < 0, dla x > 0.

Wyznaczyć dystrybuantę oraz P(0 < X < ln 2).

120. Dobrać tak stałą k, by funkcja

f(x) =

k arc sin x 0

dla x G [0, 1], poza tym

była gęstością pewnej zmiennej losowej X.

121. Zmienna losowa X ma dystrybuantę postaci

{0    dla x < 0,

3x²~2x³ x 6 (0, 1], 1    dla x > 1.

Znaleźć funkcję gęstości i narysować jej wykres. Obliczyć EX, D²X, P(0 < X < ^), P(X > g) oraz podać interpretację geometryczną tych prawdopodobieństw.

122. Dystrybuantą pewnej zmiennej losowej X jest postaci

f^0	dla x < 0,
F(x) = { X^3	dla x G (0, 1],
[l	dla x > 1.

Narysować wykres F, znaleźć funkcję gęstości, obliczyć EX, D²X, P(0 < X < g), medianę oraz a>o,2 i 20,729-

© Copyright by W. Młocek, K. Piwowarczyk and A. Rutkowska