6355786634

ści bezrobocia (stopa bezrobocia nie podwyższająca płac)place są stale, stopa ich wzrostu wynosi zero, jest to punkt równowagi na rynku pracy, czyli naturalna stopa bezrobocia

42.    W późniejszym okresie Samuelson i Solow zmodyfikowali krzywą Phillipsa i zamiast stopy wzrostu płac nominalnych wstawili inflację. Wynika z tego, że przed polityką gospodarczą soi wybór:

•    albo obniżać bezrobocie kosztem wyższej inflacji,

•    albo obniżać inflację kosztem wzrostu bezrobocia.

43.    Jednak w latach 70-tych pojawiła się stagflacja. Jednocześnie występująca wysoka inflacja oraz wysokie bezrobocie spowodowały, że zwątpiono w słuszność koncepcji Philipsa. Rozwiązanie podali monetaryści, na czele z M. Friedmanem, którzy rozróżnili krótki i długi okres.

44.    Etapy rozumowania Friedmana:

•    A - punkt początkowy to gospodarka w stanie równowagi, charakteryzująca się brakiem inflacji rzeczywistej i inflacji oczekiwanej oraz brakiem zmiany stopy plac nominalnych (W=n=rie=0%).

•    Państwo poprzez wzrost podaży pieniądza powoduje wzrost popytu na rynkach dóbr i siły roboczej; poprzez wzrost masy pieniądza rosną też ceny materiałowe i płace nominalne, ale ceny materiałowe rosną szybciej niż płace nominalne, zatem tak naprawdę płace realne maleją. Pracownicy ulegają jednak „iluzji pieniężnej” i nie widzą spadku płac realnych. Sugerując się wzrostem płac nominalnych zwiększają oni podaż siły roboczej (na którą jest popyt). Bezrobocie się zmniejsza (Uo -> Ul), przy jednoczesnym wzroście płac nominalnych ( Wo -» Wl). Tym ruchom wzdłuż krzywej Phillipsa odpowiada ruch: A —> B.

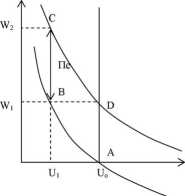
Pracownicy zdążyli się jednak zorientować, że tak naprawdę na tym (A —> B) stracili, ponieważ ich płace realne się obniżyły. Żądają dalszego wzrostu płac nominalnych, tak aby realnie nie stracić. Gdy pracodawcy się na to zgodzą, krzywa Phillipsa przesuwa się do góry i przy wyższych płacach nominalnych (W2) osiągamy punkt C położony na nowej krzywej Phillipsa. Płace nominalne będą rosły o oczekiwaną wartość inflacji (Ile) (na wyższy wzrost prawdopodobnie nie zgodzą się pracodawcy). Zatem z tego wynika, że odległość (B —» C) odpowiada wysokości Ile.