10120

Z. Kąkol-Notatki do Wykładu z Fizyki

przez idealną sprężynę jest zachowawcza. Inne siły, działają także w ten sposób, np. siła grawitacji. Gało rzucone do góry, przy zaniedbaniu oporu powietrza, wróci z tą samą prędkością i energią kinetyczną.

Jeżeli jednak ciało, na które działa jedna lub więcej sił powraca do położenia początkowego i ma inną energię kinetyczną niż na początku to oznacza, że po przebyciu drogi zamkniętej zdolność tego ciała do wykonania pracy nie została zachowana. Oznacza to, że przynajmniej jedną z działających sił określa się jako nie zachowawczą.

Aby zilustrować ten przypadek, załóżmy, że powierzchnia nie jest idealnie gładka, że mamy do czynienia z tarciem. Ta siła tarda przeciwstawia się ruchowi bez względu w którym kierunku porusza się dało (nie tak jak siła sprężystości czy grawitacji) i ciało wraca z mniejszą energią kinetyczną. Mówimy, że siła tarcia (i inne działające podobnie) są nie zachowawcze.

Możemy przeanalizować zachowawczy charakter sił analizując pracę jaką wykonuje ta siła nad punktem materialnym.

W pierwszym przykładzie (bez tarcia) praca wykonana przez siłę sprężystą, gdy sprężyna ulega ściskaniu, jest ujemna (siła jest skierowana przeciwnie do przemieszczenia, cos 180° = -1). Gdy sprężyna rozprężą się praca jest dodatnia (siła i przemieszczenie jednakowo skierowane). Podczas pełnego cyklu praca wykonana przez siłę sprężystą (siłę wypadkową) jest równa zero.

W drugim przykładzie (uwzględniamy tarcie). Praca wykonywana przez siłę tarcia jest ujemna dla każdej części cyklu (tarcie zawsze przeciwstawia się ruchowi).

Ogólnie; Siła jest zachowawcza, jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej jest równa zenr. Siła jest nie zachowawcza jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej nie jest równa zeru.

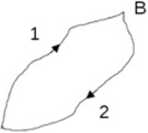
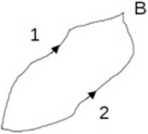
Możemy jeszcze trzecim sposobem rozważyć różnicę między siłami niezachowawczymi i zachowawczymi. Rozpatrzmy ruch z punktu A do B po jednej drodze (1) a powrót z B do A po innej (2) (patrz lysunek).

Jeżeli siła jest zachowawcza to

WaB.I ⁺    - 0

bo droga zamknięta. Możemy to zapisać inaczej

WaB.1 - - Wbą ₂

2