22904

6. Zbadać ekstrema funkcji:

a)

b)

c)

d)

e) /) 9) h)

f(x, y) = x² - xy + 2y² - x +Ay

f(x, y) = x³ + 3x²y - (iiy - 3y² - 15x - 15;/:

f(x,y) = Axy+ - + x y

}(x,y) = sin x + siu y + sin (x +;/);

f(x,y) = 1 - \A* + y²;

f(x,y) = x — 2j/ + ln \/x² + y² + 3 arctan

f(x,y) = ^⁺³> (Sx²-6xy + :iy²):

,, s A — x — y

^/(*^>ł)"7TT7+F

y.

x'

7. Wyznaczyć ekstrema lokalne podanych funkcji:

a)    /(x,9, J) = 2x² - xy + 2xz- y +y³ + z²\

b)    f(x, 9, z) = x³ + xy + y² - 2xz + 2z² + 3y - 1;

c)    f(x,y,z) =xyz(l-x-y-z);

d)    f(x,y,z)= 2— + ^—4x + 2s²;

i/ ²

e)    /(x,y,z) = (x + y + 2z)e-^f*³⁺S+*²).

8. Znaleźć ekstrema funkcji

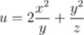
9. Znaleźć najmniejszą i największą wartość funkcji w podanych zbiorach:

<1) /(x, y) = 2x² - 2/, A' = {(1,9) : X² + y² < 4}; b) /(x, 9) = — \/4 - x² - y², K = {(x,9): z² + y² < 4}.