23835

261

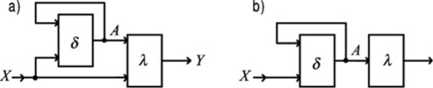
Rys.8.1. Podstawowe modele układów sekwencyjnych: a) automat Mcaly’cgo, b) automat Moorc’a

W zapisie tym każdą zmienną stanu, czyli każdy element Q_t (i = 1,2,...,k) wektora A, opisuje się równaniem

Q=S_i(Q_i,Q₂.....i.....x„)    (8.4)

Każda zmienna wyjściowa y_t(j = 1,2, może być określona przez funkcję wyjść:

-    w automacie Mealy’cgo

Y_i = \_i{Q_l,Q₂.....Q_k-,x_l,x,,...,x_n)    (8.5a)

-    w automacie Moore’a

r_j = X_J(Q_l,Q₁,...,Q_t)    (8.5b)

Blok realizujący funkcję    8 składa się z bloku pamięci

zawierającego zestaw przerzutników, czyli tzw. rejestru, oraz z układu kombinacyjnego, przygotowującego sygnały wejściowe - tzw. wektor stanu wzbudzeń elementów pamięciowych. Blok realizujący funkcję A jest układem kombinacyjnym

Dla pełnego opisu układu sekwencyjnego konieczne jest pełne określenie pięciu elementów: <A, X, Y, <5, A>. W tym celu stosuje się opis graficzny w postaci grafu zorientowanego z etykietą (nazywanego grafem przejść i wyjść), tablice przejść i wyjść oraz macierze przejść i wyjść.

Podstawą do stworzenia np. tablicy stanów, w której jest zapisany stan wyjść po takcie zegarowym dla danego stanu poprzedniego i danego stanu wejść, jest wykres stanów. Pokazuje on, jakie są stany wyjściowe układu w kolejnych cyklach zegara przy danych stanach wejściowych.

Na rys.8.2 przedstawiono bardzo prosty przykład wykresu stanów układu sekwencyjnego z jednym wejściem i dwoma wyjściami.

Przejście do kolejnych stanów wyjściowych (podanych w kolejnych okręgach) zachodzi przy stanie wejścia x = 1. Przy x = 0 układ pozostaje w stanie poprzednim.