2593

Zgodnie z założeniem zmienne losowe X_t mają ten sam rozkład co X. Stąd E(X) = ±£E(X,) = m

Znaczy to, że nieobciążonym estymatorem średniej w populacji jest średnia w próbce obserwacji.

Nie zawsze jednak funkcja próbki obserwacji jest estymatorem nieobciążonym analogicznej funkcji populacji macierzystej.

Niech X będzie zmienną losową o rozkładzie dowolnym, posiadającą drugi moment. Oznaczmy przez G² wariację zdefiniowaną jako

<r² = e(x²|-[e|x)]²    (3)

Za estymator parametru G² przyjmijmy

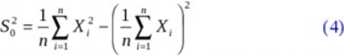
gdzie X, są niezależnymi zmiennymi losowymi o tym samym rozkładzie co X. Tak więc S₀² jest wariancją prostej próbki losowej.

E(S²) = ^E(X²)-^|E(X)]² =^(e(x²)-[£(X)|²|    (5)

n    n    n

Porównując (5) z (3) widzimy, że estymator S² zdefiniowany przez (4) jest obciążony

ze współczynnikiem obciążenia ~~~ • Ponieważ lim ~~ = 1, mówimy że Sq jest

estymatorem asymptotycznie nieobciążonym.

Dla małych wartości n obciążenie jest poważne, można je jednak łatwo usunąć. Mianowicie estymator

£x²—-— £xj =—£(x Tł n(n-l) fr n-lfe

X | (6) jest nieobciążonym

S =

1 n-ln n(n-l) estymatorem wariancji, pod warunkiem tylko, że ona istnieje.

Należy wyraźnie podkreślić, że nieobciążenie estymatora jest własnością przeciętną, której skutek objawia się przy wielokrotnym szacowaniu, Jeśli szacuje się tylko jeden raz nieznaną wariancję <r, to może zdarzyć się, że przypadkowo lepszy wynik dał wzór (4), niż

(5).

Wracając do nieobciążonego estymatora (5) warto zwrócić uwagę, że praktycy często interpretują go tak: skoro S² jest nieobciążonym estymatorem wariancji o², to S jest nieobciążonym estymatorem odchylenia standardowego a. Wniosek ten jest nieuzasadniony i zresztą błędny. Co gorsza, nie istnieje żaden estymator odchylenia standardowego, który byłby nieobdążony przy wszelkim rozkładzie w populacji macierzystej.

Efektywność estymatora.

Jeśli postać rozkładu zmiennej losowej X jest ustalona, a nie są znane wszystkie lub niektóre parametry tego rozkładu, to dla każdego parametru można wyznaczyć najmniejszą możliwą wariancję estymatora, nawet nie znając postaci tego estymatora dla rozkładu zmiennej losowej X : N(m, o).

Najmniejsza możliwa wariancja estymatora wartości oczekiwanej m wynosi o^/n, gdzie n jest liczebnością próbki. Najmniejsza możliwa wariancja estymatora wariancji <r wynosi tfUn.

37

2014-04*08