3568

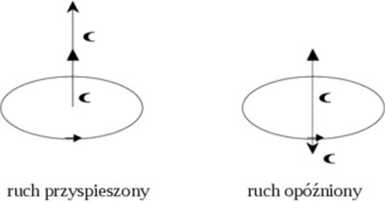
Kierunek i zwrot wektorów prędkości kątowej 0) i przyspieszenia kątowego a w ruchu obrotowym są pokazane na rysunku poniżej.

12.3 Dynamika ruchu obrotowego 12.3.1 Moment siły

W ruchu postępowym siłę wiążemy z liniowym przyspieszeniem ciała. Jaką wielkość będziemy wiązać z przyspieszeniem kątowym?

Nie może być to tylko siła bo jak pokazuje doświadczenie np. z otwieraniem drzwi przyspieszenie kątowe zależy od tego gdzie i pod jakim kątem jest przyłożona siła. W szczególności siła przyłożona w miejscu zawiasów zarówno wzdłuż jak i prostopadle do nich nie wytwarza żadnego przyspieszenia. Natomiast siła przyłożona do drzwi na ich zewnętrznej krawędzi i pod kątem prostym nadaje im maksymalne przyspieszenie.

Dla ruchu obrotowego odpowiednikiem siły w ruchu postępowym jest moment siły (tzw. moment obrotowy) %.

Jeżeli siła F działa na cząstkę to moment siły jest definiowany jako

I — I    (12.3)

gdzie wektor r reprezentuje położenie cząstki względem wybranego inercjalnego układu odniesienia. Moment siły jest wielkością wektorową, której wartość bezwzględna wynosi: X- rFsinć? (iloczyn wektorowy). Wielkość r nazywamy ramieniem siły (widać, że bierzemy albo r_x albo F_±).

12.3.2 Moment pędu

Zdefiniujmy teraz wielkość, która w mchu obrotowym odgrywa rolę analogiczną do pędu. Wielkość L będziemy nazywać momentem pędu i definiujemy ją

(12.4)

gdzie p jest pędem cząstki, a r reprezentuje położenie cząstki względem wybranego inercjalnego układu odniesienia. Wartość L wynosi rpsrnO i analogicznie do momentu siły wielkość rsind nazywamy ramieniem pędu.

2