106301

Ztrapez
KURS LICZB ZESPOLONYCH
Wzory 1: Sprowadzanie do postaci trygonometrycznej
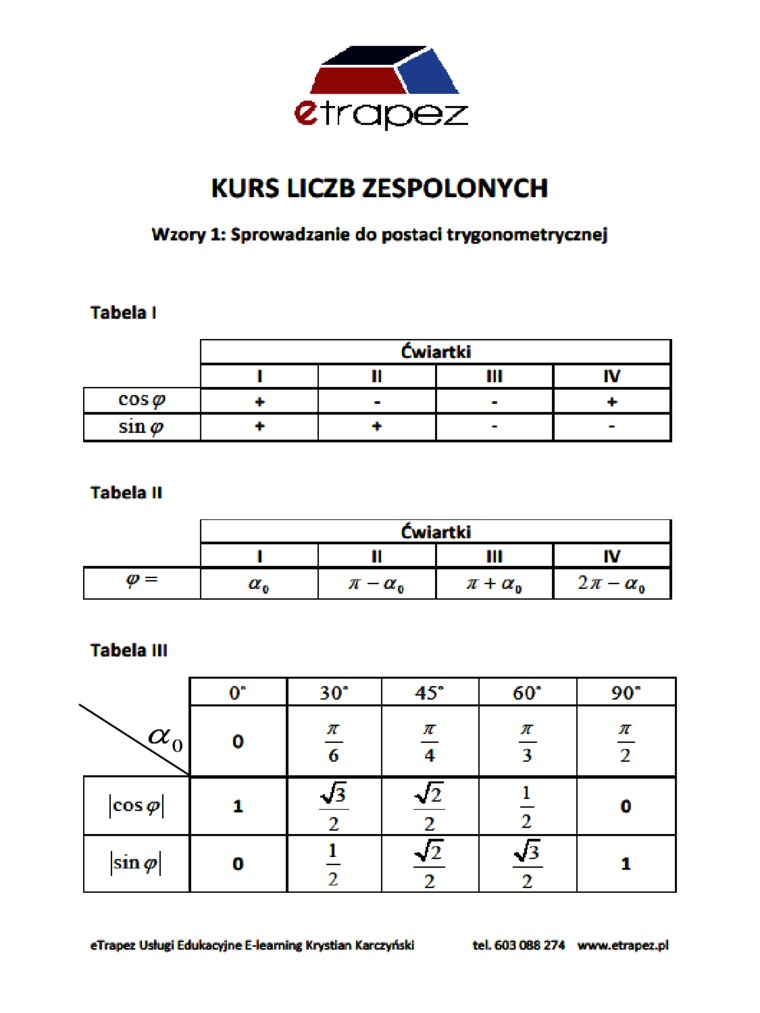
Tabela I
|
Ćwiartki | ||||
|
1 |
II |
III |
IV | |
|
cosp |
♦ |
- |
- |
♦ |
|
sinę> |
♦ |
•f |
- |
- |
Tabela II
|
Ćwiartki | ||||
|
1 |
II |
III |
IV | |
|
<P = |
<*0 |
n -ar0 |
x + a0 |
2 jr-a0 |
Tabela III
|
NsS«0 |
0' |
30‘ |
45* |
60* |
90* |
|
0 |
X ~6 |
X 7 |
X 7 |
X 7 | |
|
|cosę>| |
1 |
S 2 |
2 |
1 2 |
0 |
|
jsin^j |
0 |
1 2 |
V? 2 |
2 |
1 |
eTrapez Usługi Edukacyjne E-leaming Krystian Karczyński
te1.603 088 274 www.etrapez.pl
Wyszukiwarka
Podobne podstrony:
€ trapezKURS LICZB ZESPOLONYCH Wzory 1: Sprowadzanie do postaci trygonometrycznej Tabela
20883 str212 4. RÓWNANtA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO 212 5 2. KLASY Zadanie 2.4. Sprow
wyklad2a >Warunek nieujemności zmiennych decyzyjnych Zad. Sprowadź do postaci klasycznej i stand
skan02 1. Sprowadź do postaci kanonicznej trójmian kwadratowy a) .-r+4*-3 b)-
Badania operacyjr Zagadnienia programowania liniowego Sprowadzanie do postaci standardowej Każde
Badania operacyjr Zagadnienia programowania liniowego Przykład 1.1. Sprowadzić do postaci standardow
Badania operacyjr Zagadnienia programowania liniowegoPrzykład 1.3. Sprowadzić do postaci
111(1) Ostatnią całkę h znajdujemy osobno, wg reguły podanej w § 5. nownik sprowadzamy do postaci ka
5 Równania różniczkowe cząstkowe. Sprowadzanie do postacikanonicznej. 5.1 Sprowadzanie formy kwadrat
1REGRESJA NIELINIOWA NIELINIOWE MODELE REGRESJI SPROWADZALNE DO POSTACI LINIOWEJ Regresja nieliniowa
Funkcję x = •QC2yMÓW* , :a+B+C+^+BD+^+li + D + ABD sprowadzić do postaci „sumy raojsac w tablicy Kam
skanuj0003 1 Ćwiczenia 3 (Postać standardowa, kanoniczna, Zadanie dualne). 1. Sprowadź do postaci ka
§ 3. Zastosowania409 możemy go sprowadzić do postaci: r (x) r(x) -c+ 1 x+v)• Łatwo można się
więcej podobnych podstron