109371

Dodajemy macierze które maja jednakowe wymiary.
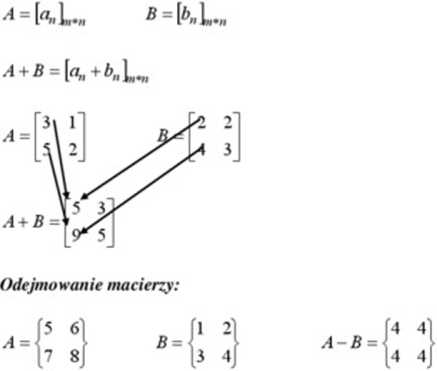
Odejmujemy macierze które maja jednakowe wymiary.
Mnoirtiif macierzy:
1. Mnożenie stałej przez mac ieiz: a* B = \a* B„
2. Mnożenie macierzy przez macierz:
Mnożenie wykonujemy w ten sposób, że wiersze I macierzy mnożymy przez kolumny II macierzy.
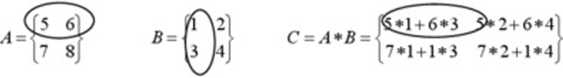
|
1 2 3' |
3 1 0' |
c„=l*3+2*2+3*6 |
c,2 = 1*1 + 2*0 + 3*l |
cl3 = 1*0+ 2*5 + 3*l | ||||||||
|
A |
4 0 1 |
B = |
2 0 5 |
C |
= A*B |
= ■ |
c2, = 4*3 + 0*2 + l*6 |
c22 = 4*1 + 0*0 +1 *1 |
c2J = 4*0 + 0*5 + l*l | |||
|
2 1 2 |
6 1 1 |
cil = 2*3+l*2+2*6 |
ci2 = 2*1 + 1*0+2*1 |
c33 = 2+0+1+5 + 2*1 | ||||||||
|
3 + 4 + 18 |
1 + 0 + 3 |
0+10 + 31 |
25 |
4 |
13 | |||||||
|
- |
12 + 0 + 6 |
4 + 0+1 |
0 + 0 + 1 |
• = |
18 |
5 |
1 | |||||
|
6+2+12 |
2 + 0+2 |
0 + 5 + 2 |
20 |
4 |
7 | |||||||
Ilość elementów w wierszu I macierzy musi być równa ilości elementów w pierwszej kolumnie II macierzy.
A =
|
j 2 i |
3\ 1 |
t^T+2*2 + 3*3> 1*1+ 2*0+3*2 |
3+4+12 1+0+6 |
19 7 | ||||
|
4 0 1 |
B = |
21 0 |
A*B = |
4*3 + 0 + 2 + l*4 4*1 + 0*0+1 * 2 |
. =. |
12+0 + 4 4 + 0 + 2 |
16 6 | |
|
2 1 2 |
4/ 2 |
2*3 + l*2+ 2*4 2*1 +1*0+ 2*2 |
6+2+8 2+0+4 |
16 6 |
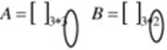
Wyszukiwarka
Podobne podstrony:
A = Odejmujemy macierze które mają jednakowe wymiary. Mnożenie macierzy: 1. Mnożenie stałej przez
m1 (7) Rozdział 2 Aby doddać lub odjąć od siebie macierze, muszą one być tych samych wymiarów,
WA308?7 II5947 NAUKA O LUDACH�609 I sztywnych.*1 które jednak zawsze kręte być mają. G u i 11 a in ■
img249 — jednakowość macierzy kowariancyjnych, — stochastyczna
17.03.2009 r. Macierze - obliczanie wyznacznika...Jak rozumieć definicję macierzy? Macierz o wymiara
TWORZENIE STRATEGII ZAKUPOWEJ Macierz Kraljica W modelu tym, na podstawie dwóch wymiarów: •
18 TWORZENIE STRATEGII ZAKUPOWEJ Macierz Kraljica Grupa „standardowe” to wszystkie kategorie, które
P3200054 obserwacji, /> zmiennych macierz X jest (/i,/?)-wymiarową macierzą danych), B = CZZC. ii
str16 (45) W szczególności, przy założeniu jednakowych odchyleń standardowych funkcji mF = mG =...=
» size(a) polecenie size zwraca wymiar macierzy »length(a) zwraca liczbę kolumn lub liczbę wierszy w
więcej podobnych podstron