121982

Układy materialne, do których odnosi się zasada zachowania energii mechanicznej, nazywamy układami zachowawczymi, a siły silami zachowawczymi. Układy, których nie dotyczy ta zasada, nazywamy układami rozpraszającymi lub dyssy-patywnymi. np. układy z tarciem.

8.    Zasada ruchu środka masy.

Środek masy układu materialnego porusza się tak jak punkt materialny o masie równej całkowitej masie układu, na który działa siła równa wektorowi głównemu sił zewnętrznych działających na ten układ, mac =W Siły wewnętrzne nie mogą zmienić ruchu środka masy ani jego położenia.

9.    Zasada pędu i zachowania pędu.

Zasada pędu punktów materialnych

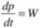
Pochodna względem czasu pędu układu punktów materialnych jest równa wektorowi głównemu sił zewnętrznych działających na ten układ.

Prawo zmietuiości pędu izasada pędu i popędu/

p(f)- p(o)= fwdt

Przyrost pędu układu materialnego w skończonym przedziale czasu jest równy popędowi wektora głównego sil zewnętrznych działających na ten układ.

Zasada zachowania pędu p=const

Jeżeli wektor główny układu sił zewnętrznych działających na układ materialny jest równy zeru. to pęd tego układu materialnego jest stały.

10. Zasada krętu i zachowania krętu.

Zasada krę tu

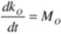
Pochodna względem czasu krętu układu punktów materialnych względem dowolnego nieruchomego punktu jest równa momentowi głównemu wszystkich sil zewnętrznych względem tego samego punktu.

Zasada zachowania krętu

ko(t)-ko(0)=0 czyli ko(t)=ko(0)=const lub jeżeli M_o=0 to ko=const

Jeżeli moment główny sił zewnętrznych względem nieruchomego punktu r edukcji O jest równy zeru. to kręt układu materialnego (bryły) względem tego punktu jest wielkością stalą.

11. Momenty bezwładności

Momentem bezw ładności punktu materialnego względem bieguna (pimktu). płaszczyzny lub osi nazywamy iloczyn masy tego pimktu i kwadratu jego odległości od bieguna, płaszczyzny lub osi.

Rodzaje momentów bezwładności:

-    biegunowe (momenty bezwładności względem punktu)

-    względem płaszczyzn

-    względem osi (osiowe momenty bezwładności)

Momenty bezwładności układu punktów materialnych

Biegunowym momentem bezwładności I_q układu punktów materialnych względem pimktu O nazywamy sumę iloczynów mas m^ i kwadratów ich odległości rk^: od punktu O, czyli j_o- y¹ ,_{Ui r}- - y + y* + _zj

Momentami bezwładności I . I . 1^ względem płaszczyzn xy, yz. zx układu punktów materialnych nazywamy sumy iloczynów mas rn przez kwadraty icli odległości od tych płaszczyzn. / = V _W| z- /^ = V m_txj /., = V m_kyj

i-i    i-i    i-i

Momentami bezwładności I, I . I względem osi x, y. z układu punktów' materialnych nazywamy sumy iloczynów mas tn oraz kwadratów' ich odległości od tych osi:

- 2 ^m*^h* = Ż ^m» fó⁺zl)

i-i    i-i

/_r = 2 ^mi^hl = Św* (z*² + x;)

i-i    i-i

i =2"»i^/»i = 2"»i (x; + y;)

Momenty dewiacyjne

Momentami dewiacyjnymi D . D . D układu punktów materialnych nazywamy sumę iloczynów mas rn^ przez iloczyn ich odległości od dwóch prostopadłych płaszczyzn yz i zx. zy i xy. xy i yz. Momenty te wyrażają wzory: