123182

WNIOSEK

4„„ jeżeli A(A) = ±(A-J,r-(A-Aj’-...-(A-A,) ' to i «, < k,

Przykład 1.

-1 0 -3 A= 3    2    3

-3 0 -1

A(A) = -(Jl-2) (A+4)

znaleźć wielomian minimalny

m(A) = -(A-2)-(A+4) m(^)=-(^-2/)-(^ + 4/)

1 CT) 1 0 m 1 1 _		i m l o		o o o
3 0 0		3 6 3	=	0 0 0
—i ro 1 O m 1 _i		i m o co 1 _1		0 0 0

=> nj(A) - wielomian anulujący Wektory główne Umowa zapisu:

W zapisie utożsamiamy wektor z jego współrzędnymi i w zależności od kontekstu v oznacza albo wektor, albo jego współrzędne w bazie.

Definicja 3.

A„.„ -macierz ^    - wartość własna macierzy

Wektor własny v odpowiadający tej wartości własnej nazywamy

wektorem głównym rzędu pierwszego i oznaczamy: v⁽¹⁾

odpowiadającego wartości własnej A jeżeli:

Wektor y¹²*,^¹"¹ * 0 nazywamy wektorem głównym rzędu drugiego

(4-/l/)(v⁽²⁾)=v⁰⁾    v^(,)*0

wektor v^<ł) * 0 nazywamy wektorem głównym rzędu k macierzy A jeżeli:

(A

V¹*"¹* * 0

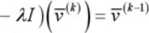
Wykład dr Magdaleny Sękowskiej strona 2 z 9 Część 13 -Wektory gł., postać Jordana