46658

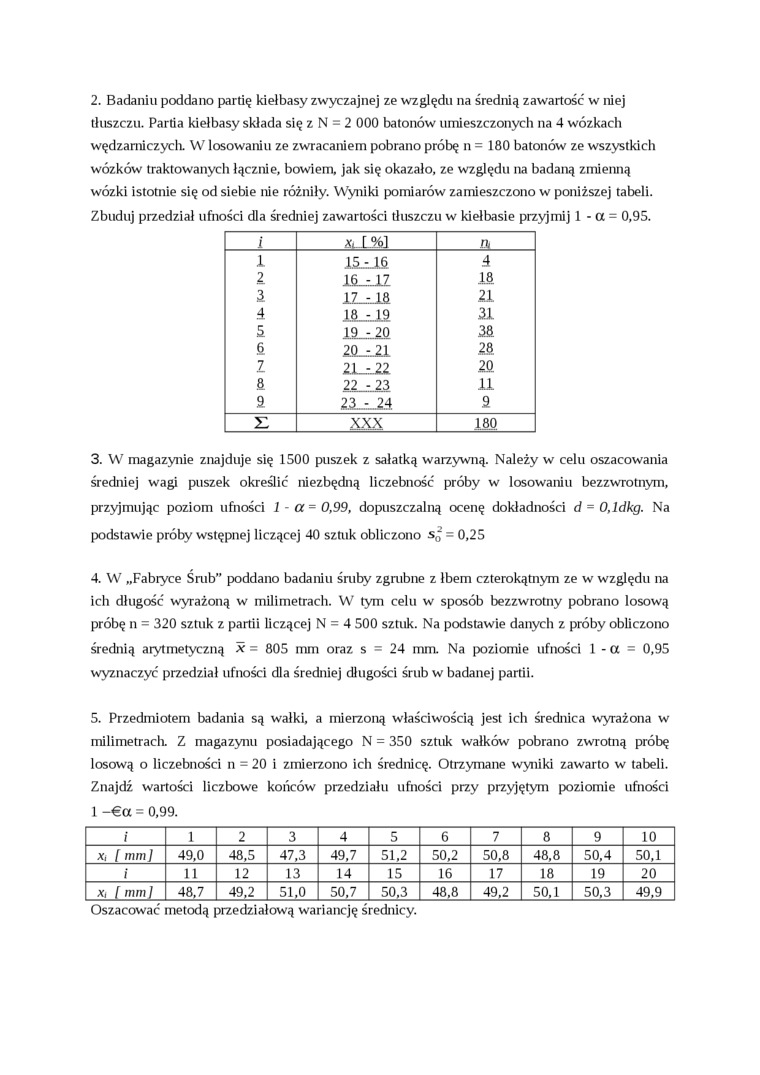
2. Badaniu poddano partię kiełbasy zwyczajnej ze względu na średnią zawartość w niej tłuszczu. Partia kiełbasy składa się z N = 2 000 batonów umieszczonych na 4 wózkach wędzamiczych. W losowaniu ze zwracaniem pobrano próbę n = 180 batonów ze wszystkich wózków traktowanych łącznie, bowiem, jak się okazało, ze względu na badaną zmienną wózki istotnie się od siebie nie różniły. Wyniki pomiarów zamieszczono w poniższej tabeli. Zbuduj przedział ufności dla średniej zawartości tłuszczu w kiełbasie przyjmij 1 - a = 0,95.

i		a
1	15-16	4
2	16-t.IZ	18
3	1Z_JL8	21
.4	13—19	31
3	19 -20	38
6	2Q_r_2l	2Sl
2	21_-..22	20
.8	22 -23	11
9	23_j_24	.9
£	XXX	180

3.    W magazynie znajduje się 1500 puszek z sałatką warzywną. Należy w celu oszacowania średniej wagi puszek określić niezbędną liczebność próby w losowaniu bezzwrotnym, przyjmując poziom ufności 1 - a = 0,99, dopuszczalną ocenę dokładności d = 0,ldkg. Na podstawie próby wstępnej liczącej 40 sztuk obliczono s£ = 0,25

4.    W „Fabryce Śrub" poddano badaniu śruby zgrubne z łbem czterokątnym ze w względu na ich długość wyrażoną w milimetrach. W tym celu w sposób bezzwrotny pobrano losową próbę n = 320 sztuk z partii liczącej N = 4 500 sztuk. Na podstawie danych z próby obliczono średnią arytmetyczną x = 805 mm oraz s = 24 mm. Na poziomie ufności 1 - a = 0,95 wyznaczyć przedział ufności dla średniej długości śrub w badanej partii.

5. Przedmiotem badania są wałki, a mierzoną właściwością jest ich średnica wyrażona w milimetrach. Z magazynu posiadającego N = 350 sztuk wałków pobrano zwrotną próbę losową o liczebności n = 20 i zmierzono ich średnicę. Otrzymane wyniki zawarto w tabeli. Znajdź wartości liczbowe końców przedziału ufności przy przyjętym poziomie ufności 1 -€a = 0,99.

Oszacować metodą przedziałową wariancję średnicy.