49668

Prawa Keplera ruchu planet

Zaiiim Newton zapostulowal prawo powszechnego ciążenia, Johannes Kepler stwierdził, że nich planet stosuje się do trzech prostych prarv. Praw^fa Keplera wzmocniły hipotezę Kopernika Praca Keplera (1609 - 1619) była wielkim odkryciem i aktem odwagi zwłaszcza po tym jak w 1600 roku spalono na stosie Giordana Bruno zwolennika systemu heliocentrycznego. Przypomnijmy, że nawet Galileusz został zmuszony do publicznego odwołania swoich poglądów (1633 r) mimo, że papież byl jego przyjacielem.

Dogmatem wtedy byl pogląd, że planety poniszają się wokół Ziemi po skomplikowanych torach, które są złożeniem pewnej liczby okręgów. Np do opisania orbity Marsa trzeba było około 12 okręgów różnej wielkości.

Kepler poszukiw-al nieskomplikowanej geometrycznie orbity, żeby udowodnić że Mars i Ziemia muszą obracać się wokół Słońca. Po latach pracy odkrył trzy proste prawa, które zgadzały się z wynikami pomiarowymi pozycji planet z bardzo dużą dokładnością Te prawa stosują się też do satelitów' okrążających jakaś planetę.

• Pierwsze prawo Keplera

Każda planeta krąży po orbicie eliptycznej, ze Sloiicem w jednym z ognisk tej elipsy

• Drugie prawo Keplera (prawo równych pól)

Linia łącząca Słońce i planetę zakreśla równe pola w równych odstępach czasu.

• Trzecie prawo Keplera

Sześciany półosi wielkich orbit dowolnych dwóch planet mają się do siebie jak kwadraty ich okresów obiegu. (Póloś wielka jest połową najdłuższej cięciwy elipsy).

R,' T.²

Dla orbit kołowych - —j

Newton rozwijając swoją teorię potrafił dowieść, że tylko wtedy, gdy siła jest odwrotnie proporcjonalna do kwadra tu odległości, orbita dowolnej planety jest elipsą ze Słońcem w jednym z R,' T.¹

ognisk oraz, że , = , . Newton wyprowadził prawa Keplera z zasad dynamiki Przykładowo

R-, 7V

wyprowadźmy III prawo Keplera dla planet poruszających się po orbitach kołowych. Korzystając z otrzymanego uprzednio wzora na masę Słońca otrzymamy dla pierwszej planety:

4t ²R[ GT²

a dla drugiej

4t '-Rl GT²

Tł

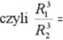
Porównując otrzymamy

Rl

Drugie praw'o Keplera wynika z zasady zachowania pędu (dowód można pominąć).