ZAS ZACH PĘD SIŁ ODŚR 3

PRAWO POWSZECHNEGO CIĄŻENIA

i stąd:

a*-*²

MZ [ UL.!* _ GT-sl ' '<    Lłks-S² - t's² “*J

Po podstawieniu wartości liczbowych:

= J6.67 I0-^,I^2^    V 10.35-I0⁵ f =1000?

f    3.WI0* ⁵

SPOSÓB II: (siła odśrodkowa bezwładności)

Na krążący wokół Ziemi Księżyc działa siła grawitacji, wynikająca ze wzajemnego przyciągania się tych dwóch ciał. Wartość siły grawitacji, zgodnie ze wzorem (2.9):

Siła ta (w układzie odniesienia związanym z krążącym Księżycem) jest równoważona przez siłę odśrodkową bezwładności (wzór (2.15)):

!'odar ~    -

Czyli zachodzi: a stąd

odsr

nr

Zauważmy, że zapisane tu równanie jest identyczne z równaniem otrzymanym przy rozwiązywaniu zadania poprzednim sposobem. Zatem w obu metodach otrzymujemy ten sam wynik.

Odn. Prędkość ruchu Księżyca po orbicie kołowej wokół Ziemi równa jest 1000 m/s.

Zadanie 2.21

ruch po orbicie kołowej

Sztuczny satelita krąży ze stalą prędkością kątową dookoła Ziemi (promień R) po orbicie kołowej o promieniu r. Obliczyć okres obiegu satelity. Obliczenia numeryczne wykonać dla r ■ 7938 km, l< = 6280 km, # = 9.8 jy.

Dane:    r - 7938 km = 7.938 • I O⁶ m

R = 6280km =6.28 -JO⁶ m S=9.S1^

Szukane:

7'= ? - okres obiegu satelity

Pomiędzy krążącym wokół Ziemi satelitą, a Ziemią działa siła grawitacji o wartości (patrz wzór (2.9)):

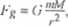
gdzie m jest masą satelity, M - masą Ziemi, r • odległością pomiędzy satelitą a środkiem Ziemi. Siła ta (w układzie związanym z Ziemią) pełni rolę siły dośrodkowej, której wartość, zgodnie ze wzorem (2.13), można zapisać następująco:

Fdtur ■

gdzie to jest prędkością kątową ruchu satelity po okręgu o promieniu r. Do zapisania siły dośrodkowej stosujemy w tym przypadku wzór, w którym występuje prędkość

kątowa o>, gdyż prędkość ta jest powiązana z okresem ruchu po okręgu zależnością (1.33):

»«^jr

Jak już wspomniano, siła grawitacji h'_K równa jest sile dośrodkowej :

fll * ^tknr

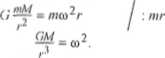
Wprowadzamy do powyższej zależności okres 7‘ i wyznaczamy go:

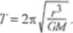
Choć wyznaczyliśmy szukany okres 7, nie jest to koniec rozwiązywania zadania. Został w mm umieszczony "haczyk”. Zamiast wartości liczbowych O (stała grawitacji) i M (masa Ziemi) w danych podano wartość N (promień Ziemi) i g (przyspieszenie ziemskie). Wyraźmy więc iloczyn OM poprzez g i R Dla dała o masie m umieszczonego na powierzchni Ziemi zachodzi (wzór (2.10):

GM-gR².

czyli:

Stąd:

Po podstawieniu wartości liczbowych:

Odn. Okres obiegu satelity równy jest 7141 s, to jest około 2 h.

s * 7141 s a 2h.

71