ZAS ZACH PĘD SIŁ ODŚR 1

ZASADA ZACHOWANIA PĘDU

ZASADA ZACHOWANIA PĘDU

Zadanie 2.15

zetknięcie się dwóch ciał w ruchu

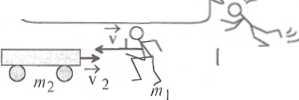
Człowiek o masie my = 60 kg, biegnący z prędkością v₍ = 8 km/h, dogania wózek o masie 90 kg, który jedzie z prędkością V2 = 4 km/h i wskakuje na ten wózek; a) z jaką prędkością będzie poruszał się wózek z człowiekiem? b) Jaka będzie prędkość wózka z człowiekiem w przypadku, gdy człowiek będzie biegł naprzeciw wózka?

Po im:

vj =8 km/h v₂ = 4 km/h m | =60 kg w 2 = 90 kg

Szukane:

prędkość układu wózek + człowiek dla sytuacji opisanej w podpunkcie

a)    v« - ?

b) v_A«?

"M

przed skokiem

a) Z zasady zachowania pędu wynika, że pęd układu człowiek + wózek będzie taki sam w obu sytuacjach: przed wskoczeniem człowieka na wózek i po wskoczeniu.

Pamiętając o tym, że pęd układu ciał równy jest sumie wektorowej pędów

poszczególnych ciał, otrzymamy zgodnie z równaniem (2.6): ^m\ ^v I ^+w2 ^v2 ⁼ (^ml ^+m2) ^vo-

Jest to równanie wektorowe i należ) je przekształcić do równania skalarnego. W tym przypadku wektory my v ₍i /w₂ v ₂ mają ten sam kierunek i zwrot, a więc można zapisać dla długości tych wektorów następującą zależność:

#W|V| +f»2^v2 = (^mi +n» 2)^v<** z której otrzymujemy wynik końcowy:

v_a =

®2^V2

>l+«2

k«

km

km _ 5 ^ ton h    h

Po podstawieniu wartości liczbowych:

60-8+90-4

Vo =

60+90

b) W podpunkcie tym człowiek i wózek poruszają się w przeciwnych kierunkach. Po wskoczeniu człowieka na wózek, ten ostatni może poruszać się w dotychczasowym kierunku, może też zmienić kierunek ruchu na przeciwny. Na początku rozwiązywania zadania zwykle nie wiemy, która z tych dwóch możliwości wystąpi. Należy więc wybrać w dowolny sposób jedną z nich i rozwiązać całe zadanie konsekwentnie dla tego przypadku. Wynik końcowy pokaże, czy nasze założenie było słuszne. Zasada zachowania pędu będzie miała w tym przypadku następującą postać (patrz wzór (2.6)):

A*| V|+»₂V2«(II,+*2)V*

A ja chciałem w przeciwnym kierunku

TT~0

m\ +/W2 po skoku

przed skokiem

Wektory w, v , i m₂v 2 "“W zwroty przeciwne. Należy jeden z tych zwrotów przyjąć za dodatni i korzystając z tego sprowadzić powyższe równanie wektorowe do równania skalarnego dla długości wektorów: Gdy za dodatni uznamy kierunek ruchu wózka, to równanie skalanie będzie miało następującą postać:

(-m,v,) + m₂V2 - («, +i»₂)v*.

Z powyższego równania wyznaczamy szukaną wartość :

. *2^V? ~**l^vl 1    «, *m₂

Po podstawieniu wartości liczbowych:

Vf-0.8 lf.

Otrzymaliśmy wartość prędkości v_A ujemną, zatem nasze wstępne założenie o kierunku ruchu wózka po skoku człowieka było błędne. W rzeczywistości po wskoczeniu człowieka na wózek kierunek ruchu wózka się zmieni i będzie zgodny z kierunkiem ruchu człowieka. Wspomnijmy tylko na zakończenie, że gdyby uczynione na wstępie założenie co do kierunku ruchu wózka było prawdziwe. 10 otrzymalibyśmy wartość prędkości v_A większą od zera.

(kip. W przypadku, gdy człowiek i wózek poruszają się w tym samym kierunku, prędkość wózka po wskoczeniu człowieka wynosi S.6 km/h. W przypadku przeciwnych kierunków ruchu prędkość końcowa równa jest 0.8 km/h i jest skierowana zgodnie z kierunkiem ruchu człowieka przed wskoczeniem.

Zadanie 2.16

rozpad dała w ruchu

Granat lecący w pewnej chwili z prędkością v • 10 m/s rozerwał się na dwa odłamki. Większy odłamek, którego masa stanowiła w = 60% masy całego granatu, kontynuował lot w pierwotnym kierunku, lecz ze zwiększoną prędkością V| = 2Sm/s. Znaleźć kierunek i wartość prędkości mniejszego odłamka.

Dane:	Szukane:
v- 10®	v 2 ■ ?- kierunek i wartość prędkości
w-60%	mniejszego odłamka po wybuchu
*l-25f

7a*wU zachowania pędu mówi nam. że pęd granatu przed wybuchem musi być równy sumie pędów wszystkich odłamków granatu po wybuchu, czyli:

67