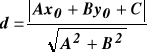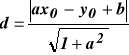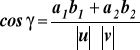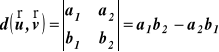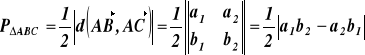VIII. GEOMETRIA ANALITYCZNA
|
|
|
2. Równość wektorów |
3. Długość wektora |
4. Działania na wektorach |
5. Cosinus kąta między wektorami |
6. Iloczyn skalarny wektorów |
7. Warunek prostopadłości wektorów |
8. Warunek równoległości wektorów |
9. Wyznacznik pary wektorów |
10. Pole trójkąta ABC |
|
2. Równanie prostej przechodzącej przez dwa różne punkty A = (xA, yA) i B = (xB, yB) |
3. Równanie ogólne prostej |
4. Warunek równoległości prostych |
5. Warunek prostopadłości prostych |
6. Warunek równoległości prostych |
7. Warunek prostopadłości prostych |
|
|
47
Wyszukiwarka
Podobne podstrony:
geometria analityczna
Geometria analityczna przyklady
GEOMETRIA ANALITYCZNA
Planimetria i geometria analityczna zadania
01 Geometria analityczna w n wymiarach okładka
Algebra 0 18 geometria analityczna
04 Geometria analityczna wektory
geometria analityczna, MATURA, Matematyka, Poziom podstawowy
Planimetria i geometria analityczna zadania, Zadania na studia z matematyki
3222142 d viii geometria analit Nieznany (2)
Algebra 0 16 geometria analityczna
geometria analityczna zadania
matma- geometria analityczna- powtórka, Do Matury, Matematyka
Test z geometrii analityczej, szkoła ponadgimnazjalna
Geometria analityczna, Matematyka dla Szkoły Podstawowej
Geometria analityczna cz1, Technikum, Matematyka
Zestawy zadań matma, Geometria analityczna, dr Anna Barbaszewska-Wiśniowska
nacobezu geometria analityczna rozszerzenie
więcej podobnych podstron