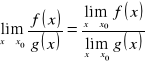Definicje i twierdzenia na ustny egzamin maturalny z matematyki
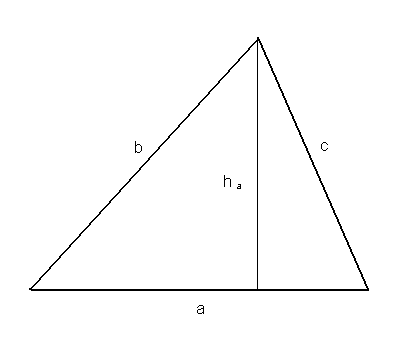
1. Twierdzenie sinusów (tw. Snelliusa)
Tw.
Dla dowolnego trójkąta stosunek długości boku do sinusa kąta leżącego naprzeciw jest stały i równa się podwojonej długości promienia okręgu opisanego na tym trójkącie.
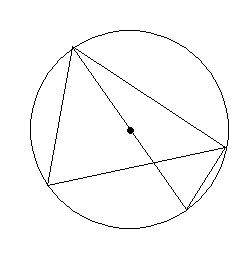
![]()
Dowód:
Z twierdzenia, że kąty wpisane oparte na tym samym łuku mają równe miary:
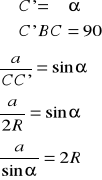
c.n.d.
2. Twierdzenie cosinusów (tw. Carnota, uogólnienie tw. Pitagorasa)
Tw.
W dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków przez cosinus kąta zawartego między nimi.
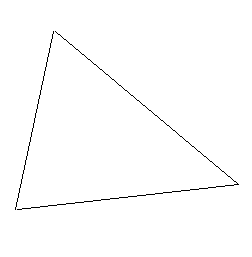
a2 = b2 + c2 - 2bc*cosα
b2 = a2 + c2 - 2ac*cosβ
c2 = a2 + b2 - 2ab*cosγ
Dowód 1:
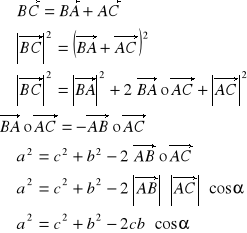
c.n.d.Dowód 2:
Na mocy twierdzenia sinusów boki a, b, c są proporcjonalne do odpowiednio sinα, sinβ, sinγ. Twierdzenie cosinusów przybierze zatem postać:
sin2α = sin2β + sin2γ - 2 sinβ sinγ cosα
Z twierdzenia o sumie kątów w trójkącie :
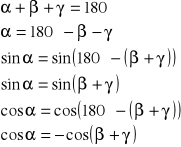
Lewa strona równania (I):
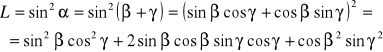
Prawa strona równania (I):
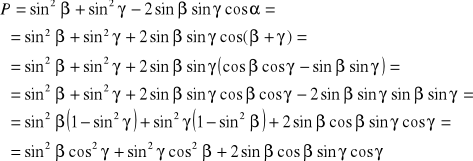
L = P c.n.d.
Wnioski z twierdzenia cosinusów:
1.
![]()
2. Twierdzenie Pitagorasa
![]()
3.
![]()
3. Twierdzenie o wysokości w trójkącie prostokątnym
Tw.
Wysokość poprowadzona z wierzchołka kąta prostego trójkąta jest średnią geometryczną długości odcinków na jakie dzieli przeciwprostokątną.
(W trójkącie prostokątnym kwadrat wysokości opuszczonej na przeciwprostokątną jest równy iloczynowi długości odcinków, na które dzieli tą przeciwprostokątną)
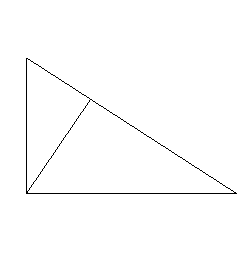
![]()
( h2 = pq )
Dowód:
Z podobieństwa trójkątów:
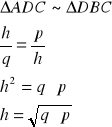
c.n.d.
4. Twierdzenie o czworokącie opisanym na okręgu
Tw.
Czworokąt wypukły można opisać na okręgu wtedy i tylko wtedy gdy sumy długości przeciwległych boków w tym czworokącie są równe.
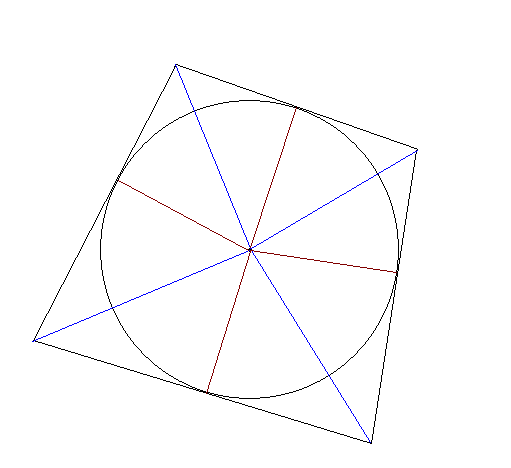
Teza:
|BC| + |AD| = |AB| + |CD|
Dowód:
Zauważamy przystawanie par trójkątów:

Wtedy:
|AB| = u + x
|BC| = x + y
|CD| = y + z
|DA| = z + u
L = |BC| + |AD| = x + y + z + u
P = |AB| + |CD| = u + x + y + z
L = P
c.n.d.
5. Twierdzenie o czworokącie wpisanym w okrąg
Tw.
Czworokąt wypukły można wpisać w okrąg wtedy i tylko wtedy, gdy sumy miar przeciwległych kątów w tym czworokącie są równe i wynoszą 180° (π).
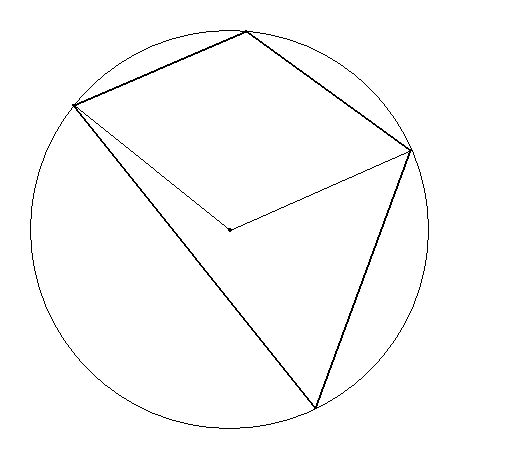
Teza:
α + β = γ + δ = 180° = π
Dowód:
Korzystając z twierdzenia o kącie środkowym i wpisanym w okrąg:
2α + 2β = 2π /:2
α + β = π
c.n.d.
6. Twierdzenie o odległości dwóch dowolnych punktów koła
Tw.
Odległość dwóch dowolnych punktów koła jest niewiększa od jego średnicy.
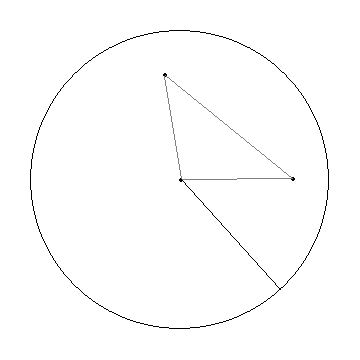
Teza:
![]()
Dowód:
Z definicji koła:
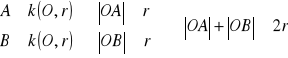
(po dodaniu nierówności stronami)
Z twierdzenia o długościach boków trójkątów:
![]()
Z własności nierówności:
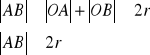
c.n.d.
7. Twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie
Tw.
Rzuty dwóch boków trójkąta w kierunku dwusiecznej kąta wewnętrznego zawartego miedzy tymi dwoma bokami są proporcjonalne do długości tych boków.
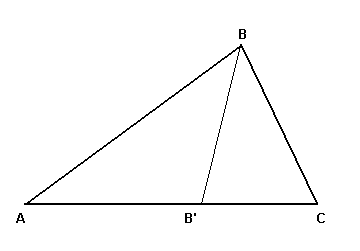
Dowód:
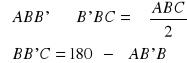
Z twierdzenia sinusów:
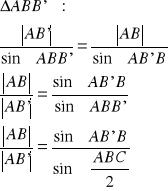
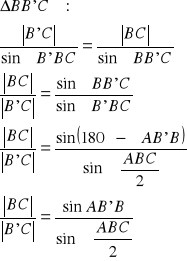
c.n.d.
8/9. Twierdzenie o kącie środkowym i wpisanym w okrąg
Tw.
Miara kąta środkowego jest dwa razy większa od miary kąta wpisanego opartego na tym samym łuku.
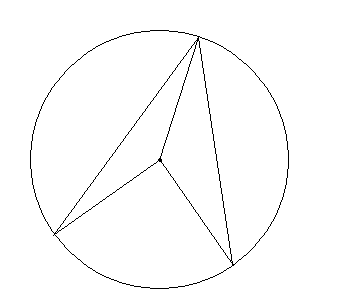
założenie:
β = γ + δ
teza:
α = 2β
dowód:

c.n.d.
10. Twierdzenie o symetralnych boków trójkąta
Tw.
W dowolnym trójkącie wszystkie trzy symetralne jego boków przecinają się w jednym punkcie, który jest środkiem okręgu opisanego na tym trójkącie.
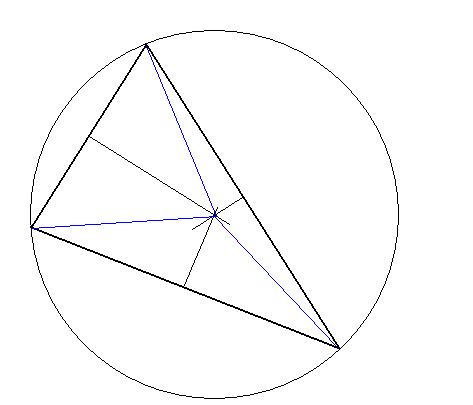
założenie:
ΔABC
teza:
![]()
dowód:
korzystając z def. symetralnej odcinka (zbiór punktów równo oddalonych od końców odcinka)
c.n.d.
11. Twierdzenie o dwusiecznych kąta
Tw.
W dowolnym trójkącie wszystkie trzy dwusieczne jego kątów przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt.
założenia:
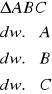
teza:
![]()
dowód:
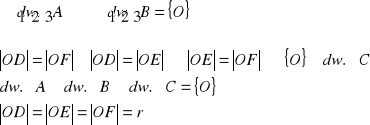
z def. dwusiecznej kąta (zbiór punktów równo oddalonych od prostych, w których zawierają się ramiona kąta)
c.n.d.
12. Twierdzenie Pitagorasa
Tw.
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
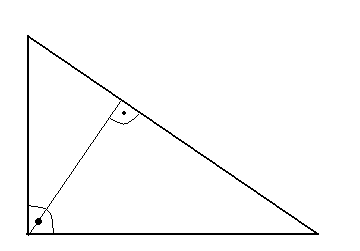
a2 + b2 = c2
założenie:
![]()
dowód 1:
dowód 2:
ΔBDC i ΔABC są podobne o skali podobieństwa ![]()
;
ΔADC i ΔABC są podobne o skali podobieństwa ![]()
.
Oznaczmy pole ΔABC przez P, pole ΔBDC przez P1 i pole ΔADC przez P2
Ponieważ stosunek pól figur podobnych jest równy kwadratowi skali prawdopodobieństwa otrzymujemy:
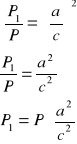
![]()
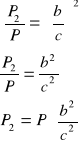
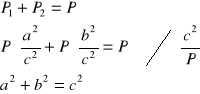
c.n.d.
dowód 3:
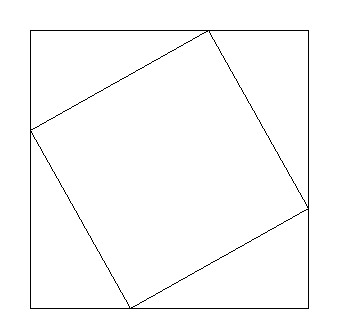
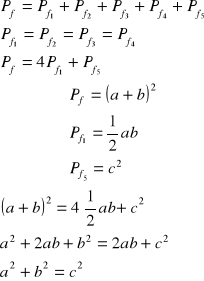
c.n.d.
13. Twierdzenie o środkowych boków trójkąta
Tw.
W dowolnym trójkącie wszystkie trzy środkowe jego boków przecinają się w jednym punkcie, który jest środkiem ciężkości tego trójkąta. Punkt ten dzieli każdą ze środkowych na odcinki o stosunku długości 2:1.
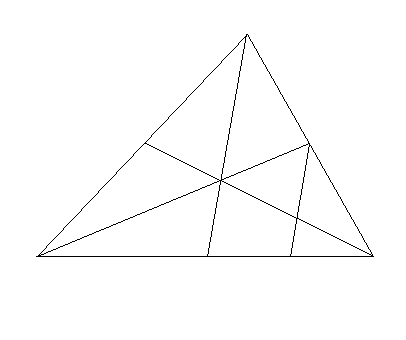
założenia:
środkowe ![]()
![]()
teza:
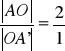
dowód:
z twierdzenia Talesa dla kąta ![]()
:
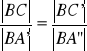
z założenia:
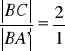
zatem:
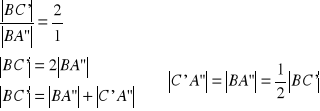
z twierdzenia Talesa dla kąta ![]()
:
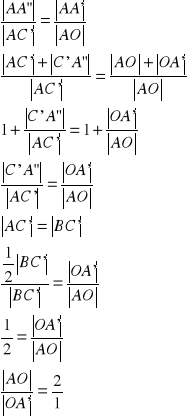
c.n.d.
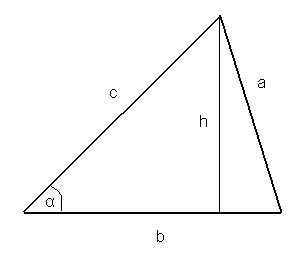
14. Wzory na pole trójkąta
![]()
dowód:

![]()
![]()
c.n.d.
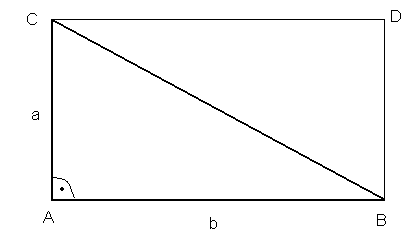
II.
W trójkącie prostokątnym:
![]()
dowód:
c.n.d.
III.
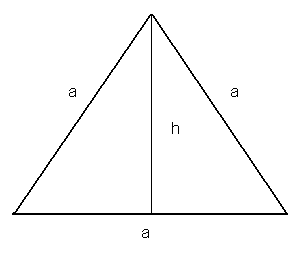
W trójkącie równobocznym:
![]()
dowód:
z twierdzenia Pitagorasa:
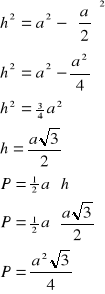
c.n.d.
IV.
![]()
dowód:
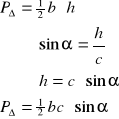
c.n.d.
(pozostałe dowodzi się analogicznie)
V.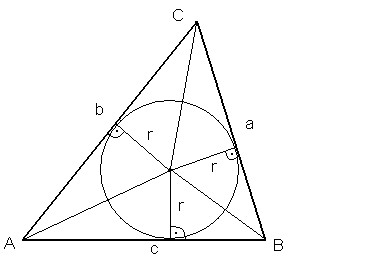
![]()
dowód:
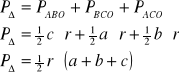
c.n.d.
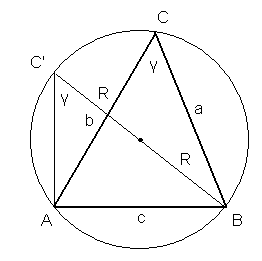
VI.
![]()
dowód:
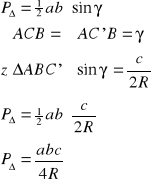
udowodnione wyżej
z twierdzenia o kątach opartych na tym samym łuku
z tw.o kątach wpisanym i środkowym ΔABC' jest
prostokątny
c.n.d.
VII.
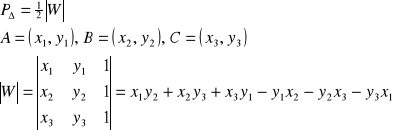
VIII.
Wzór Herona:
![]()
15. Twierdzenie o podzielności wielomianu przez dwumian (tw. Bezout)
Tw.
Wielomian W(x) dzieli się bez reszty przez dwumian x-p wtedy i tylko wtedy gdy p jest pierwiastkiem wielomianu W(x).
dowód:
Niech p będzie pierwiastkiem wielomianu W(x). Dzieląc z resztą wielomian W przez x-p otrzymujemy :
W(x)=(x-p)V(x)+R
gdzie V(x) to pewien wielomian, zaś R - liczba.
Podstawiając za x=p otrzymujemy:
0=W(p)=(p-p)V(p)+R
stąd R=0, czyli W(x) dzieli się przez x-p.
Niech teraz wielomian W(x) dzieli się przez x-p. Wtedy:
W(x)=(x-p)V(x)
Podstawiając x=p mamy:
W(p)=(p-p)V(p)=0
czyli p jest pierwiastkiem wielomianu W(x)
c.n.d.
16. Twierdzenie na wyraz ogólny ciągu arytmetycznego
Tw.
an=a1+(n-1)r
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L=a1
P= a1+(1-1)r= a1
L=P
II
założenie indukcyjne dla n=k :
ak= a1+(k-1)r
teza indukcyjna dla n=k+1 :
ak+1= a1+kr
dowód:
z def:
ak+1 - ak=r
ak+1= ak+r
zał.ind.
ak+1= a1+(k-1)r +r
ak+1= a1+kr-r +r= a1+kr c.n.d.
17. Twierdzenie na wyraz ogólny ciągu geometrycznego
Tw.
an=a1·qn-1
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L=a1
P= a1·q1-1= a1
L=P
II
założenie indukcyjne dla n=k :
ak= a1·qk-1
teza indukcyjna dla n=k+1 :
ak+1= a1·qk
dowód:
z def:
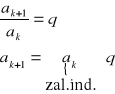
ak+1 = a1·qk-1·q = ak+1= a1·qk c.n.d.
18. Wzór na sumę n początkowych wyrazów ciągu arytmetycznego
Tw.
![]()
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L= S1= a1
![]()
L=P
sprawdzenie dla n=2:
L= S2= a1+ a2
![]()
L=P
II
założenie indukcyjne dla n=k :
![]()
teza indukcyjna dla n=k+1 :
![]()
dowód:
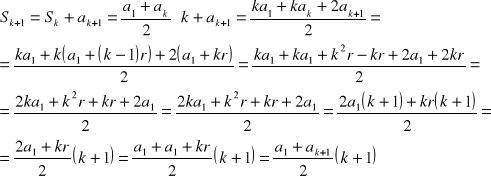
c.n.d.
19. Wzór na sumę n początkowych wyrazów ciągu geometrycznego
Tw.
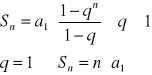
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L= S1= a1
![]()
L=P
sprawdzenie dla n=2:
L= S2= a1+ a2
![]()
L=P
II
założenie indukcyjne dla n=k :
![]()
teza indukcyjna dla n=k+1 :
![]()
dowód:
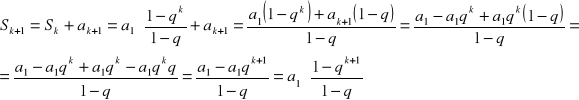
c.n.d.
20. Twierdzenia o działaniach na logarytmach
I.
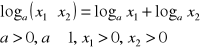
dowód:
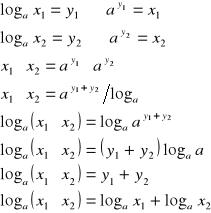
c.n.d.
II.
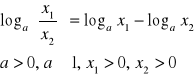
dowód:
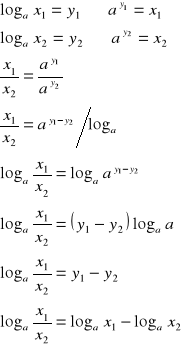
c.n.d.
III.
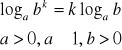
dowód:
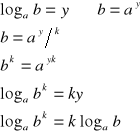
c.n.d.
IV.
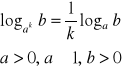
dowód:
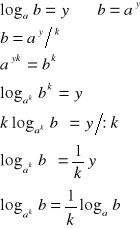
c.n.d.
V.
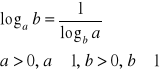
dowód:
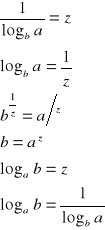
c.n.d.
VI.
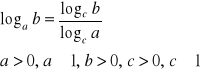
dowód:
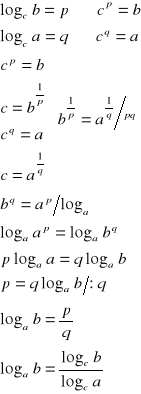
c.n.d.
VII.
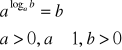
dowód: (niewprost)
sprzeczność, zatem wzór jest prawdziwy c.n.d.
21. Twierdzenie o pochodnej iloczynu i ilorazu dwóch funkcji
Tw.
Pochodna iloczynu dwóch funkcji jest równa sumie iloczynów pochodnej pierwszej funkcji przez funkcję drugą oraz pierwszej funkcji przez pochodną drugiej funkcji.
![]()
dowód:
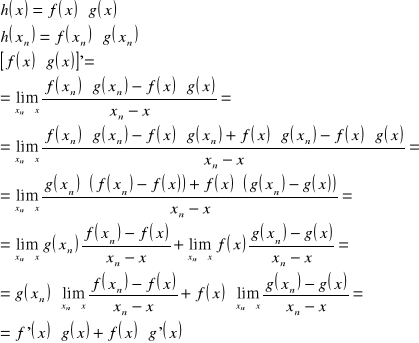
c.n.d.
Tw.
Pochodna ilorazu dwóch funkcji jest równa ilorazowi różnicy iloczynów pochodnej pierwszej funkcji przez funkcję drugą oraz pochodnej drugiej funkcji przez funkcję pierwszą, przez kwadrat funkcji drugiej.
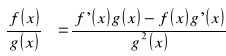
dowód:
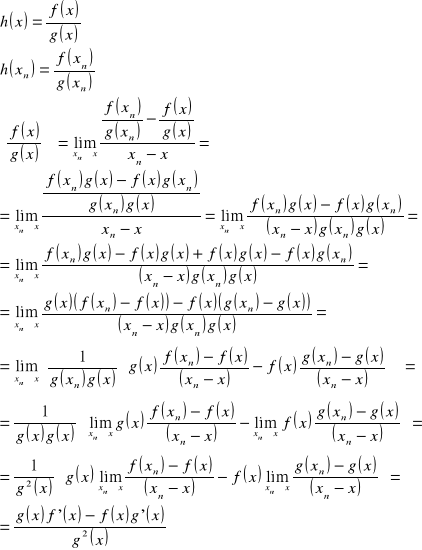
c.n.d.
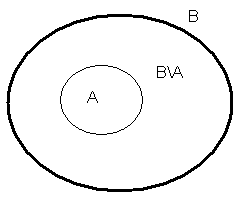
22. Własności prawdopodobieństwa
Niech Ω będzie danym zbiorem zdarzeń elementarnych, niech P będzie prawdopodobieństwem określonym na zdarzeniach ![]()
. Wówczas:
I.
![]()
dowód:
korzystamy ze wzorów ![]()
na mocy warunku definicji prawdopodobieństwa, że![]()
otrzymujemy:
![]()
c.n.d.
II.
![]()
dowód:
![]()
zbiory A i B\A są rozłączne
na mocy warunku definicji prawdopodobieństwa, że ![]()
otrzymujemy:
![]()
c.n.d.
III.
![]()
dowód:
z udowodnionej własności II: ![]()
z warunku definicji prawdopodobieństwa, że ![]()
otrzymujemy:
![]()
c.n.d.
IV.
![]()
dowód:
korzystając ze wzoru ![]()
oraz warunków definicji prawdopodobieństwa, że
![]()
otrzymujemy:
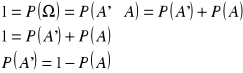
c.n.d.
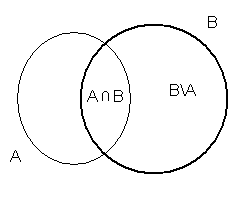
V.
![]()
dowód:
korzystamy z tożsamości :
![]()
ponieważ
![]()
więc na mocy warunku definicji prawdopodobieństwa, że
![]()
otrzymujemy:
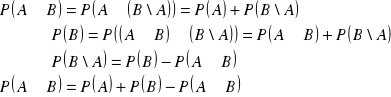
c.n.d.
23. Twierdzenie o prostej prostopadłej do płaszczyzny
Tw.
Jeżeli prosta jest prostopadła do dwóch przecinających się prostych to jest prostopadła do płaszczyzny w której się te dwie proste zawierają.
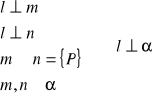
dowód:
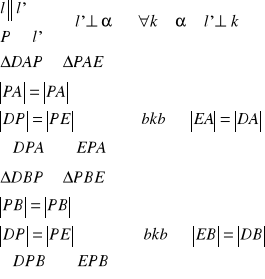

c.n.d.
24. Twierdzenie o trzech prostopadłych
Tw.
Jeżeli prosta l należąca do płaszczyzny α jest prostopadła do rzutu prostej pochyłej k względem tej płaszczyzny, to prosta l jest prostopadła do tej pochyłej.
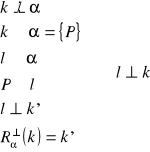
dowód:
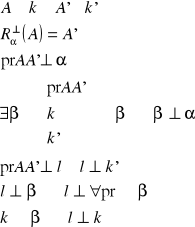
c.n.d.
25. Twierdzenie o pierwiastkach wymiernych wielomianu
Tw.
Jeżeli wszystkie współczynniki wielomianu a0, a1, a2,..., an są całkowite, a liczba wymierna zapisana w postaci ułamka nieskracalnego ![]()
jest pierwiastkiem równania
anxn+...+ a2x2+ a1x+ a0=0
to p jest dzielnikiem a0, natomiast q jest dzielnikiem an.
dowód:
z założenia mamy:
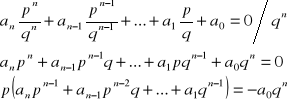
Lewa strona otrzymanej równości dzieli się przez p oraz p i q nie mają wspólnych dzielników więc p i qn również nie mają wspólnych dzielników zatem a0 dzieli się przez p.
Przez symetrię prawdziwa jest i druga teza twierdzenia.
c.n.d.
26. Twierdzenie o dwusiecznej kąta zewnętrznego w trójkącie
Tw.
Rzuty dwóch boków trójkąta w kierunku dwusiecznej kąta zewnętrznego przyległego do danego kąta są proporcjonalne do długości tych boków.
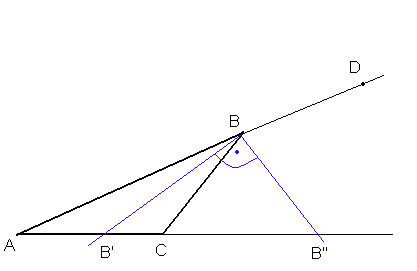
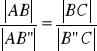
dowód:
![]()
z twierdzenia sinusów:
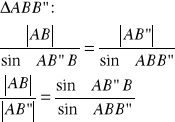
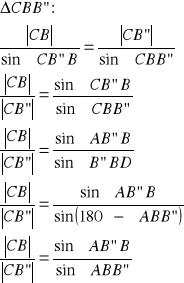
![]()
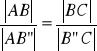
c.n.d.
27. Definicje działań na zbiorach, przedziałów liczbowych, zbiorów ograniczonych i kresów
Definicje działań na zbiorach
I.
Suma
Sumą ![]()
zbiorów A i B nazywamy zbiór złożony z wszystkich elementów zbioru A i wszystkich elementów zbioru B i z żadnych innych.
![]()
II
Iloczyn
Iloczynem ![]()
zbiorów A i B nazywamy zbiór złożony z tych i tylko tych elementów, które należą jednocześnie do zbioru A oraz do zbioru B.
![]()
III
Różnica
Różnicą ![]()
zbiorów A i B nazywamy zbiór złożony z tych i tylko tych elementów zbioru A, które nie należą do zbioru B.
![]()
IV
Różnica symetryczna
Różnicą symetryczną![]()
zbiorów A i B nazywamy zbiór złożony z tych i tylko tych elementów, które należą do zbioru A i nie należą do zbioru B, lub należą do zbioru B i nie należą do zbioru A.
![]()
V
Dopełnienie
Dopełnieniem A' zbioru A nazywamy zbiór złożony z tych i tylko tych elementów, które nie należą do zbioru A.
![]()
VI
Zawieranie się zbiorów
![]()
VII
Równość zbiorów
![]()
Definicje przedziałów liczbowych
I.
Otwarty
Przedział otwarty (a, b) to zbiór wszystkich takich liczb ![]()
, że a<x i x<b.
![]()
II.
Domknięty
Przedział domknięty ![]()
to zbiór wszystkich takich liczb ![]()
, że a≤x i x≤b.
![]()
III.
Lewostronnie domknięty
Przedział lewostronnie domknięty ![]()
to zbiór wszystkich takich liczb ![]()
, że a≤x i x<b.
![]()
IV.
Prawostronnie domknięty
Przedział prawostronnie domknięty ![]()
to zbiór wszystkich takich liczb ![]()
, że a<x i x≤b.
![]()
Definicje zbiorów ograniczonych
I.
z dołu
Zbiór A nazywamy ograniczonym z dołu gdy istnieje liczba n niewiększa od każdego ![]()
II.
z góry
Zbiór A nazywamy ograniczonym z góry gdy istnieje liczba n niemniejsza od każdego ![]()
Zbiór ograniczony zarówno z dołu jak i z góry nazywamy ograniczonym.
Definicje kresów
I.
kres górny
Kresem górnym zbioru A nazywamy najmniejszą liczbę ograniczającą zbiór A z góry.
sup A (supremum zbioru A)
II.
kres dolny
Kresem dolnym zbioru A nazywamy największą liczbę ograniczającą zbiór A z dołu.
inf A (infimum zbioru A)
28. Określenie funkcji, definicje funkcji monotonicznych, parzystych, nieparzystych, okresowych
Określenie funkcji
Funkcją f odwzorowującą zbiór X w zbiór Y nazywamy przyporządkowanie każdemu elementowi x zbioru X dokładnie jednego elementu y zbioru Y.
Definicje funkcji monotonicznych
I.
rosnąca
Funkcję f nazywamy rosnącą jeżeli f(x1)< f(x2), gdy x1< x2
![]()
jest rosnąca
![]()
jest rosnąca
II.
niemalejąca
Funkcję f nazywamy niemalejącą jeżeli f(x1)≤ f(x2), gdy x1< x2
![]()
jest niemalejąca
![]()
jest niemalejąca
III.
malejąca
Funkcję f nazywamy malejącą jeżeli f(x1)> f(x2), gdy x1< x2
![]()
jest malejąca
![]()
jest malejąca
IV.
nierosnąca
Funkcję f nazywamy nierosnącą jeżeli f(x1)≥ f(x2), gdy x1< x2
![]()
jest nierosnąca
![]()
jest nierosnąca
V.
stała
Funkcję f nazywamy stałą jeżeli f(x1)= f(x2), gdy x1< x2
![]()
jest stała
![]()
jest stała
Definicje innych rodzajów funkcji
I.
funkcja parzysta
Funkcję f nazywamy parzystą jeżeli dla każdego x należącego do dziedziny funkcji f spełniony jest warunek f(-x) = f(x).
![]()
Wykres funkcji parzystej jest symetryczny względem osi OY.
II.
funkcja nieparzysta
Funkcję f nazywamy nieparzystą jeżeli dla każdego x należącego do dziedziny funkcji f spełniony jest warunek f(-x) = - f(x).
![]()
Wykres funkcji nieparzystej jest symetryczny względem początku układu współrzędnych
III.
funkcja okresowa
Funkcję f nazywamy okresową, gdy istnieje taka liczba s ≠ 0, że dla każdej liczby x z dziedziny funkcji f liczba x+s należy do tej dziedziny i f(x+s)=f(x).
![]()
Liczba s jest okresem tej funkcji. Najmniejszy okres dodatni, jeżeli istnieje, nazywamy okresem zasadniczym.
29. Funkcja liniowa, równania liniowe - dyskusja liczby pierwiastków
def.
Funkcją liniową nazywamy funkcję postaci:
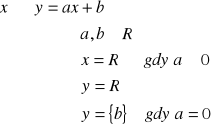
![]()
f. stała y = b
![]()
f. rosnąca
![]()
f. malejąca
funkcja liniowa jest w całej dziedzinie monotoniczna
gdy a≠0 posiada jedno miejsce zerowe ![]()
![]()
α - kąt przecięcia wykresu z osią OX
a - współczynnik kierunkowy
def.
Równaniem liniowym nazywamy równanie postaci:
![]()
I.
równanie jest oznaczone (1 rozwiązanie) ![]()
![]()
II.
równanie jest sprzeczne (0 rozwiązań) ![]()
III.
równanie jest nieoznaczone czyli tożsamościowe (nieskończenie wiele rozwiązań) ![]()
![]()
def.
Równaniem liniowym z dwiema niewiadomymi nazywamy równanie postaci:
Ax+By+C=0
30. Funkcja kwadratowa, wzory, postacie, pierwiastki, dyskusja liczby i jakości pierwiastków w zależności od parametru
def.
Funkcją kwadratową nazywamy funkcję postaci:
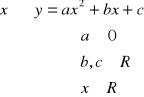
(trójmian kwadratowy)
Postacie funkcji kwadratowej:
I.
ogólna:
![]()
![]()
- wyróżnik trójmianu kwadratowego
II.
kanoniczna:
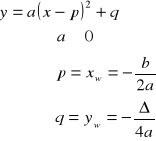
III.
iloczynowa:
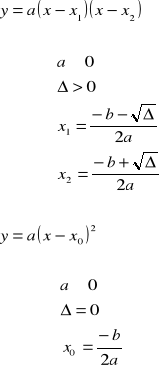
Wzory na pierwiastki funkcji kwadratowej
Pierwiastki funkcji kwadratowej to odcięte punktów przecięcia paraboli z osią x.
Dyskusja liczby pierwiastków:
I.
dwa różne pierwiastki ![]()
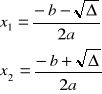
II.
jeden pierwiastek podwójny![]()
![]()
III.
brak pierwiastków ![]()
Wzory Viete'a
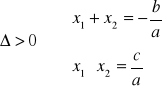
dowód:
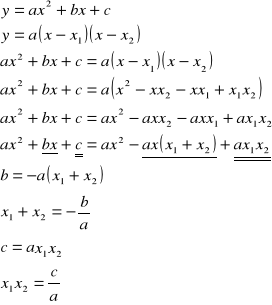
c.n.d.
Dyskusja jakości pierwiastków:
I.
dwa pierwiastki różnych znaków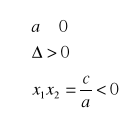
II.
dwa różne pierwiastki ujemne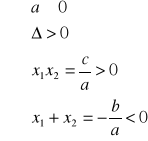
III.
dwa różne pierwiastki dodatnie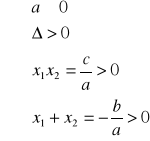
IV.
dwa pierwiastki tego samego znaku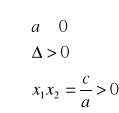
V.
jeden pierwiastek podwójny dodatni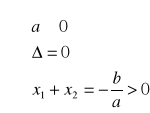
VI.
jeden pierwiastek podwójny ujemny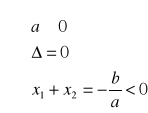
31. Układ równań liniowych, dyskusja liczby rozwiązań
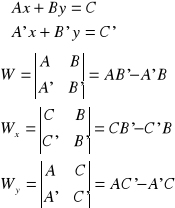
Wzory Cramera:
![]()
Dyskusja liczby rozwiązań:
I.
układ równań jest niezależny (jedna para rozwiązań) ![]()
II.
układ równań jest zależny (nieskończenie wiele par rozwiązań) ![]()
III.
układ równań jest sprzeczny (brak rozwiązań) ![]()
32. Wartość bezwzględna
def.
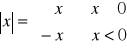
własności:
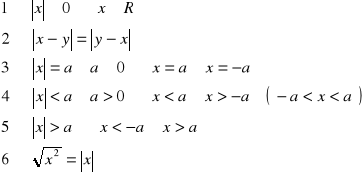
33. Funkcja homograficzna, definicje i wykres
def.
Funkcja homograficzna to funkcja wymierna zmiennej x określona wzorem:
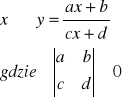
dziedzina:
![]()
funkcja ta jest funkcją liniową i X=R
![]()
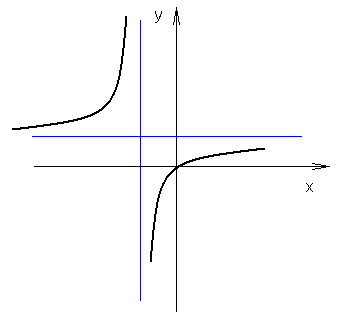
wykres:
Wykresem funkcji homograficznej jest hiperbola ![]()
przesunięta o wektor ![]()
gdzie:
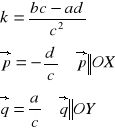
![]()
równanie asymptoty poziomej
![]()
równanie asymptoty pionowej
34. Funkcja potęgowa, wykładnicza i logarytmiczna, trygonometryczna, definicje, wykresy i własnosci
Funkcja potegowa
def.
Funkcją potegową nazywamy funkcję postaci:
![]()
wykresy:
I. ![]()
![]()
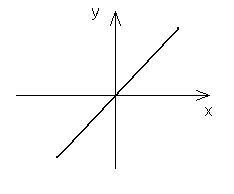
![]()
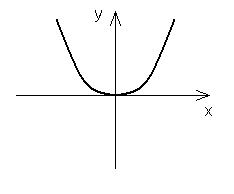
dla n parzystych:
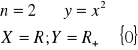
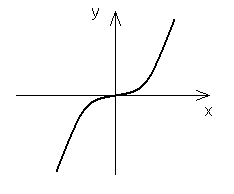
dla n nieparzystych:
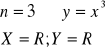
II. ![]()
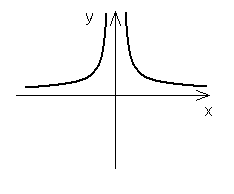
dla n parzystych:
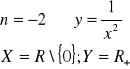
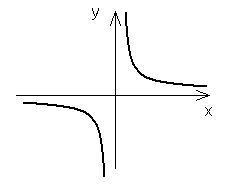
dla n nieparzystych:
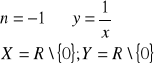
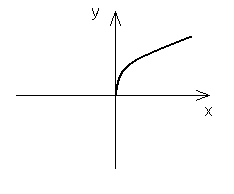
III. ![]()
dla k parzystych:
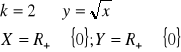
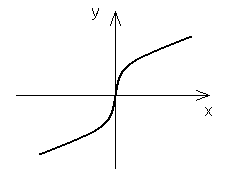
dla k nieparzystych:
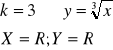
IV. ![]()
dla k parzystych:
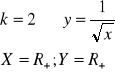
dla k nieparzystych:
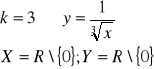
Funkcja wykładnicza
def.
Funkcją wykładniczą nazywamy funkcję postaci:
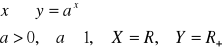
I.
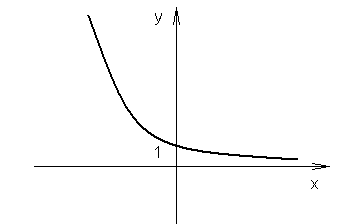
0<a<1
np. 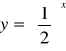
własności:

II.
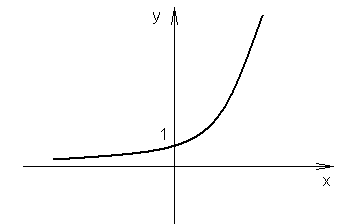
a>1
np. ![]()
własności:

Funkcja logarytmiczna
def. logarytmu
![]()
Logarytmem o dodatniej i różnej od 1 podstawie a z liczby logarytmowanej b większej od 0 nazywamy wykładnik potęgi c, do której należy podnieść podstawę a aby otrzymać liczbe logarytmowaną b.
def.
Funkcją logarytmiczną nazywamy funkcję postaci:
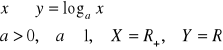
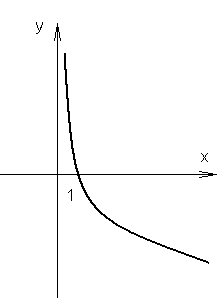
I.
0<a<1
np. ![]()
własności:
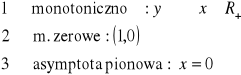
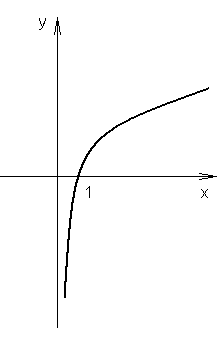
II.
a>1
np. ![]()
własności:
Funkcje trygonometryczne
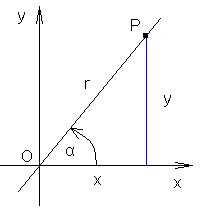
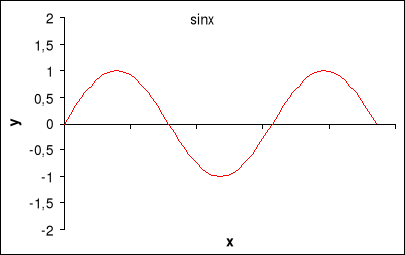
def.
Jeżeli α jest miarą kąta skierowanego ![]()
, P jest dowolnym punktem końcowego ramienia tego kąta (![]()
), x i y są współrzędnymi P, ![]()
, to:
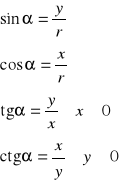
I.
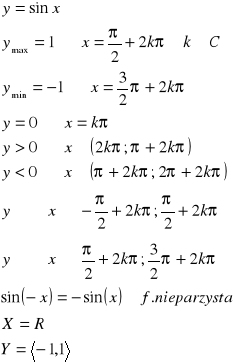
II.

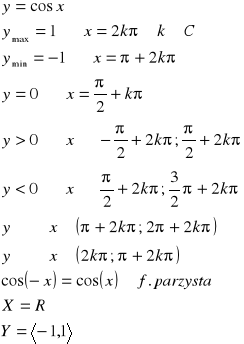
III.

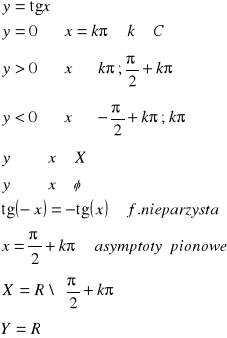
IV.

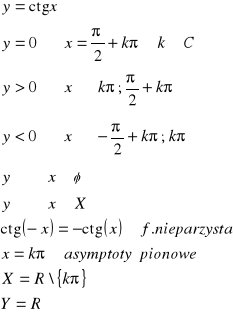
35. Ciąg liczbowy, monotoniczność
def.
Ciągiem liczbowym nazywamy funkcję określoną na zbiorze liczb naturalnych i o wartościach rzeczywistych.
a1, a2, a3,…, an,
monotoniczność ciągu:
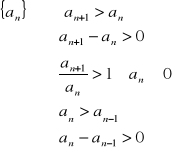
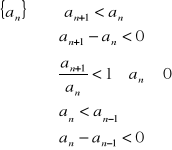
36. Ciąg arytmetyczny, geometryczny, definicje, wzory, własności
Ciąg arytmetyczny
def.
Ciąg liczbowy w którym różnica pomiędzy wyrazem dowolnym i poprzednim (z wyjątkiem wyrazu pierwszego) jest stała i równa się r.
![]()
wzory:
n-ty wyraz ciągu
![]()
suma n elementów
![]()
3 kolejne elementy (warunek ciągu arytmetycznego)
![]()
monotoniczność:
![]()
rośnie ![]()
![]()
maleje ![]()
![]()
jest stały ![]()
Ciąg geometryczny
def.
Ciąg liczbowy w którym iloraz wyrazu dowolnym przez poprzedni (z wyjątkiem wyrazu pierwszego) jest stała i równa się q.
![]()
ciąg geometryczny zbieżny (do zera)
![]()
wzory:
n-ty wyraz ciągu
![]()
suma n elementów
![]()
suma wszystkich elementów ciągu zbieżnego
![]()
dowód:
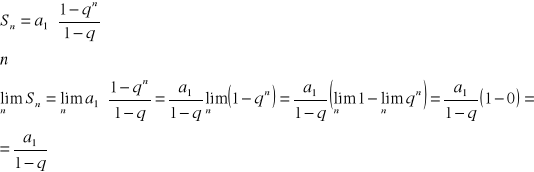
c.n.d.
3 kolejne elementy
![]()
monotoniczność:
Ciąg geometryczny ![]()
jest:
naprzemienny
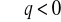
rosnący
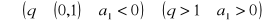
malejący
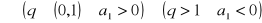
stały
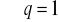
37. Definicje ilorazu różnicowego, pochodnej funkcji w punkcie i ich interpretacje.
Iloraz różnicowy
def.
Iloraz różnicowy jest to iloraz przyrostu wartości do przyrostu argumentów.
![]()
I.
![]()
II.
![]()
III.
![]()
interpretacja geometryczna
Iloraz różnicowy jest to tangens kąta jaki tworzy prosta (sieczna) przecinająca wykres funkcji w dwóch punktach, ze zwrotem dodatnim osi OX.
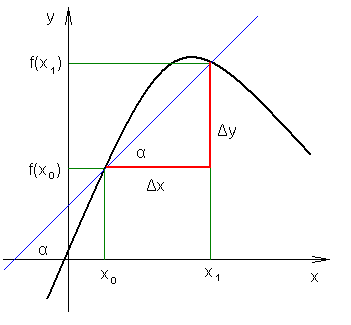
![]()
Pochodna funkcji w punkcie
def.
Dana jest funkcja y=f(x) gdzie ![]()
oraz punkt ![]()
, ![]()
, gdzie xn jest dowolnym ciągiem ![]()
takim, że ![]()
.
Pochodna funkcji w punkcie to granica do której dąży ciąg ilorazów różnicowych.
I.
![]()
II.
![]()
III.
![]()
IV.
![]()
interpretacja geometryczna
Pochodna funkcji w punkcie o odciętej x0 jest to tangens kąta jaki tworzy styczna do wykresu funkcji w punkcie o odciętej x0 ze zwrotem dodatnim osi OX.
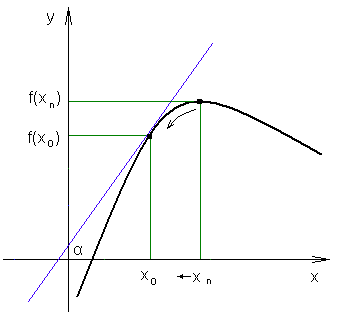
![]()
38. Granica funkcji, ciągłość funkcji, definicje, twierdzenia.
Granica ciągu
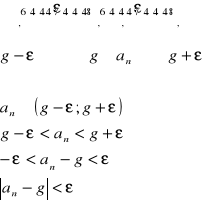
def.
Ciąg an ma granicę g wtedy i tylko wtedy, gdy w dowolnym ε-lonowym otoczeniu liczby g znajdują się prawie wszystkie wyrazy ciągu an.
![]()
Granica funkcji w punkcie
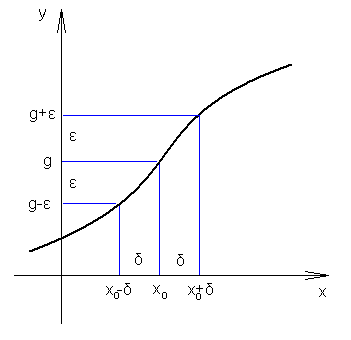
sąsiedztwo ![]()
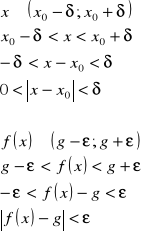
def. granicy funkcji w punkcie wg Cauchy'ego
![]()
def. granicy funkcji w punkcie wg Heine'go (ciągowa)
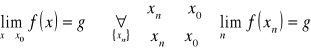
def. granicy lewostronnej funkcji w punkcie wg Cauchy'ego
![]()
def. granicy lewostronnej funkcji w punkcie wg Heine'go
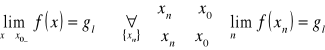
def. granicy prawostronnej funkcji w punkcie wg Cauchy'ego
![]()
def. granicy prawostronnej funkcji w punkcie wg Heine'go
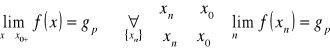
Własności granicy funkcji
Ciągłość funkcji
def. ciągłości funkcji w punkcie
Funkcja y=f(x) jest ciągła w punkcie x0 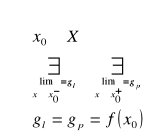
def. ciągłości funkcji w punkcie wg Cauchy'ego
Funkcja jest ciągła w punkcie x0 gdy:
![]()
def. funkcji ciągłej w przedziale otwartym
Funkcja y=f(x) jest ciągła w przedziale otwartym wtedy i tylko wtedy gdy jest ciągła w każdym punkcie tego przedziału
def. funkcji ciągłej w przedziale zamkniętym
Funkcja y=f(x) jest ciągła w przedziale zamkniętym ![]()
wtedy i tylko wtedy gdy jest ciągła w (a,b), a ![]()
i ![]()
Własności funkcji ciągłych:
Tw.1.
zał:
f(x), g(x) są ciągłe w swojej dziedzinie
1. ![]()
jest ciągła
2. ![]()
jest ciągła
3. ![]()
jest ciągła
4. ![]()
jest ciągła
Tw.2.
Jeżeli funkcja y=f(x) jest ciągła i ściśle monotoniczna dla ![]()
jest ciągła i ściśle monotoniczna dla ![]()
Tw. o ciągłości funkcji złożonej
Dana jest funkcja złożona ![]()
Jeżeli funkcja f(x) jest ciągła w punkcie x0, a funkcja g(u) też jest ciągła w punkcie u0, gdzie u0=f(x0) to funkcja ![]()
jest ciągła w punkcie x0.
Tw. o możliwości wprowadzenia granicy do funkcji ciągłej
Jeżeli istnieje granica właściwa ![]()
oraz funkcja ![]()
jest ciągła w punkcie u0=f(x0) to ![]()
39. Asymptoty wykresu funkcji, wzory na pochodne, pochodna a monotoniczność funkcji
Asymptoty
def.
Asymptota to prosta o tej własności, że gdy punkt oddala się nieograniczenie od punktu (0,0) po wykresie, to jego odległość od tej prostej dąży do zera.
asymptota pionowa
Prostą o równaniu x=x0 nazywamy asymptotą pionową krzywej o równaniu y=f(x), jeśli lewo- lub prawostronna granica funkcji w tym punkcie jest niewłasciwa, tzn.
![]()
Jeżeli obie te granice są niewłaściwe asymptota jest obustronna. Jeżeli tylko jedna z nich - jednostronna.
asymptota ukośna
Prostą o równaniu y=ax+b nazywamy asymptotą ukośną krzywej o równaniu y=f(x), jeśli a i b są tak dobrane, że:
![]()
tzn.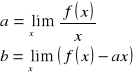
asymptota pozioma
Asymptota pozioma jest szczególnym przypadkiem asymptoty ukośnej, gdzie ![]()
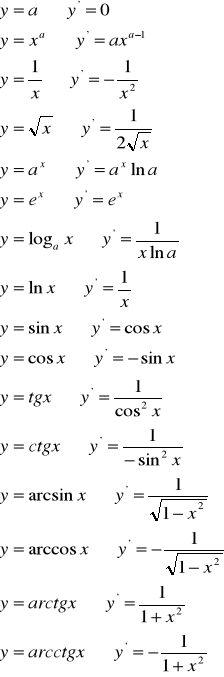
Wzory na pochodne
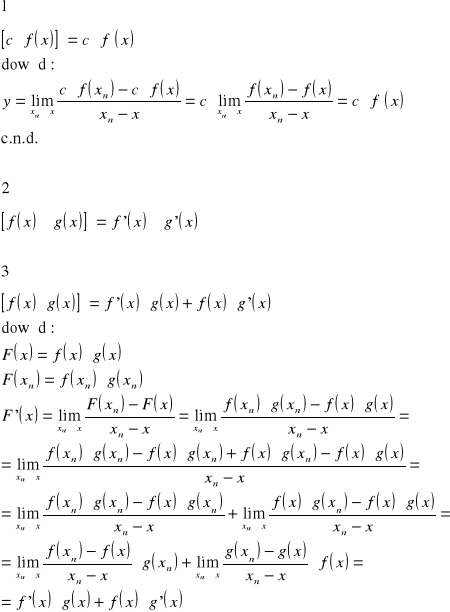
c.n.d.
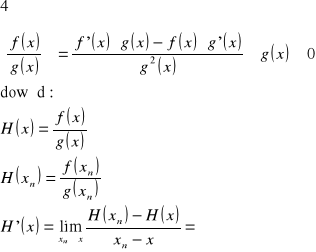

c.n.d.
![]()
Pochodna funkcji złożonej
Dana jest funkcja F(x)=f(g(x)).
Załóżmy, że funkcja g jest różniczkowalna w punkcie x oraz funkcja f jest różniczkowalna w punkcie g(x).
Wówczas:
F'(x)=f'(g(x)) g'(x)
Pochodna a monotoniczność funkcji
I.
Jeżeli funkcja f(x) jest różniczkowalna w pewnym przedziale (a,b) i dla każdego
![]()
lub dla skończonej liczby argumentów
![]()
II.
Jeżeli funkcja f(x) jest różniczkowalna w pewnym przedziale (a,b) i dla każdego
![]()
lub dla skończonej liczby argumentów
![]()
40. Ekstremum funkcji, definicje i reguły badania ekstremów
Maksimum i minimum noszą wspólną nazwę ekstremum funkcji.
Ekstremum właściwe
def.1.
minimum właściwe
Funkcja y=f(x) posiada w punkcie x0 minimum właściwe![]()
maksimum właściwe
Funkcja y=f(x) posiada w punkcie x0 maksimum właściwe![]()
def.2.
Jeżeli w pewnym otoczeniu punktu ![]()
funkcja f jest różniczkowalna i z lewej strony punktu x0 f'(x)>0, a z prawej jego strony f'(x)<0 (pochodna zmienia znak z + na-), to funkcja f ma w punkcie x0 maksimum właściwe. f'(x0)=0
Jeżeli zaś w pewnym otoczeniu punktu ![]()
funkcja f jest różniczkowalna i z lewej strony punktu x0 f'(x)<0, a z prawej jego strony f'(x)>0(pochodna zmienia znak z - na+), to funkcja f ma w punkcie x0 minimum właściwe. f'(x0)=0
Ekstremum lokalne
Jeżeli w pewnym niezerowym otoczeniu punktu x0, f(x0) jest największą wartością funkcji f(x) w tym otoczeniu, to w punkcie x0 istnieje maksimum lokalne funkcji f(x)
Jeżeli w pewnym niezerowym otoczeniu punktu x0, f(x0) jest najmniejszą wartością funkcji f(x) w tym otoczeniu, to w punkcie x0 istnieje minimum lokalne funkcji f(x)
Reguły badania ekstremum:
I.
Warunek konieczny istnienia ekstremum funkcji
Jeżeli funkcja f(x) ma w punkcie x0 ekstremum i jest różniczkowalna w tym punkcie to f'(x)=0
(twierdzenie odwrotne jest fałszywe)
II.
Warunek wystarczający istnienia ekstremum funkcji
I.
Zał. y=f(x) jest ciągła w punkcie x0 i jest różniczkowalna w jego sąsiedztwie ![]()
1.
![]()
w punkcie x0 jest
maksimum właściwe
2.
![]()
w punkcie x0 jest
minimum właściwe
II.
Jeżeli funkcja y=f(x) ma w otoczeniu ![]()
ciągłe pochodne f'(x0) i f”(x0) i f”(x0)≠0
![]()
w punkcie x0 funkcja f(x) posiada maksimum
![]()
w punkcie x0 funkcja f(x) posiada minimum
41. Definicje i wzory na liczbę permutacji, kombinacji, wariacji, dwumian Newtona
Permutacją bez powtórzeń zbioru n- elementowego A={a1, a2,..., an}nazywamy każdy n- wyrazowy ciąg utworzony ze wszystkich elementów tego zbioru, czyli każde uporządkowanie elementów zbioru A.
![]()
Permutacją z powtórzeniami zbioru n- elementowego A={a1, a2,..., an}, w której element a1 występuje n1 razy, element a2 występuje n2 razy,..., element an występuje nk razy, przy czym n1+n2+...+nk=n, nazywamy każdy
n- wyrazowy ciąg, w którym element ai występuje ni razy dla i=1, 2,...,k.
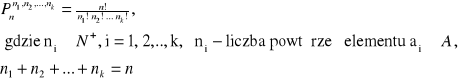
Kombinacją k- elementową bez powtórzeń zbioru n- elementowego A={a1, a2,..., an} ![]()
nazywamy każdy podzbiór k- elementowy tego zbioru.
![]()
Kombinacją k- elementową z powtórzeniami zbioru n- elementowego A={a1, a2,..., an} nazywamy każdy ciąg
(k1, k2,..., kn) taki, że k1+k2+...+kn=k, gdzie ki∈N dla i=1, 2,..., n
![]()
wariacją k- elementową bez powtórzeń zbioru n- elementowego A={a1, a2,..., an} ![]()
nazywamy każdy
k- wyrazowy ciąg różnowartościowy, którego wyrazami są elementy danego zbioru.
![]()
Wariacją k- elementową z powtórzeniami zbioru n- elementowego A={a1, a2,..., an} nazywamy każdy k- wyrazowy ciąg , którego wyrazami są elementy danego zbioru.
![]()
Symbol Newtona
![]()
Dwumian Newtona
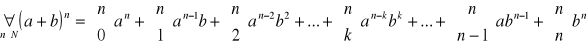
42. Definicje: zdarzenia, prawdopodobieństwa, własności, prawdopodobieństwo warunkowe, całkowite, niezależność pary zdarzeń, schemat Bernoulli'ego (zmienna losowa, wartość oczekiwana i wariancja M)
Zdarzeniem elementarnym nazywamy wynik pewnego doświadczenia
(oznaczamy ![]()
)
Zdarzeniem nazywamy podzbiór zbioru zdarzeń elementarnych (oznaczamy A, B, ...).
Przestrzenią zdarzeń elementarnych Ω nazywamy zbiór wszystkich zdarzeń elementarnych.
Definicje prawdopodobieństwa:
Klasyczna - La Place'a
Jeżeli zdarzenia elementarne są jednakowo prawdopodobne
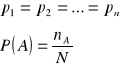
nA - liczba zdarzeń elementarnych sprzyjających zdarzeniu A
N - liczba wszystkich zdarzeń elementarnych
Aksjomatyczna
Niech Ω będzie przestrzenią zdarzeń elementarnych.
Zdarzenia ![]()
jeżeli:
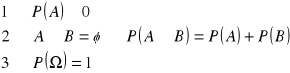
to na zbiorze Ω określone jest prawdopodobieństwo P(A).
Prawdopodobieństwo warunkowe
def.
![]()
tw.
Prawdopodobieństwo warunkowe jest określone na zdarzeniach zbioru Ω.
(spełnia def. aksjomatyczną, tzn spełnia 3 aksjomaty)
dowód:
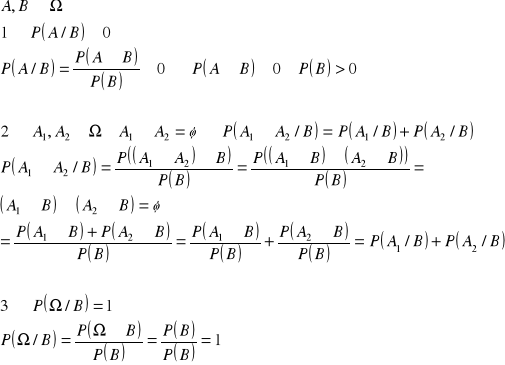
Prawdopodobieństwo całkowite
Tw.
Ω - przestrzeń zdarzeń elementarnych
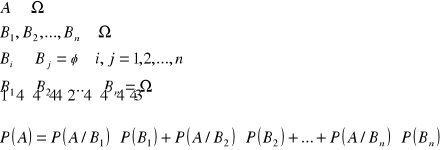
dowód:
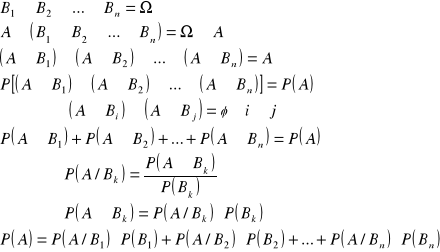
c.n.d.
Zdarzenia niezależne
Dwa zdarzenia ![]()
są niezależne ![]()
Schemat Bernoulli'ego
Prawdopodobieństwo k sukcesów w N próbach określa wzór:
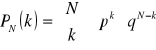
gdzie:
p - prawdopodobieństwo sukcesu w jednej próbie (jednakowe dla wszystkich prób)
q - prawdopodobieństwo porażki w jednej próbie q=1-p
N - liczba prób
k - liczba sukcesów
Najbardziej prawdopodobna liczba sukcesów w schemacie Bernoulli'ego
k0 - najbardziej prawdopodobna liczba sukcesów
![]()
jest ułamkiem wymiernym (nie jest liczbą całkowitą)
wtedy ![]()
- cecha liczby
![]()
jest liczbą całkowitą
to ![]()
Zmienna losowa
Zmienną losową X nazywamy funkcję określoną na zdarzeniach zbioru Ω i o wartościach rzeczywistych.
Rozkład zmiennej losowej
Rozkład zmiennej losowej to zbiór uporządkowanych par, w których pierwszy element pary xi jest wartością zmiennej losowej, a drugi pi jest prawdopodobieństwem z jakim ta wartość zachodzi.
![]()
Wartość oczekiwana
(nadzieja matematyczna)
![]()
xi - wartość zmiennej losowej
pi - prawdopodobieństwo z jakim zachodzi wartość zmiennej losowej
Wartość oczekiwana w schemacie Bernoulli'ego
![]()
dowód:
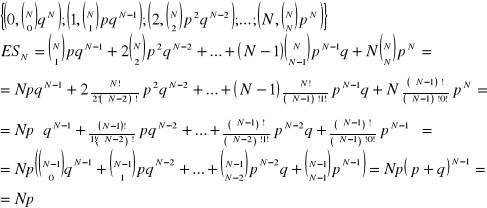
c.n.d.
Wariancja zmiennej losowej
Wariancja zmiennej losowej to miara rozrzutu zmiennej losowej.
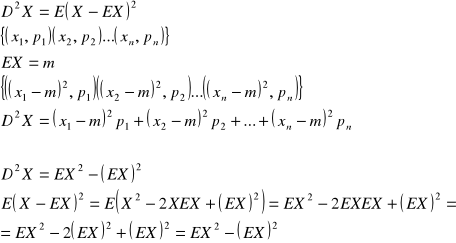
Wariancja zmiennej losowej w schemacie Bernoulli'ego
![]()
dowód:
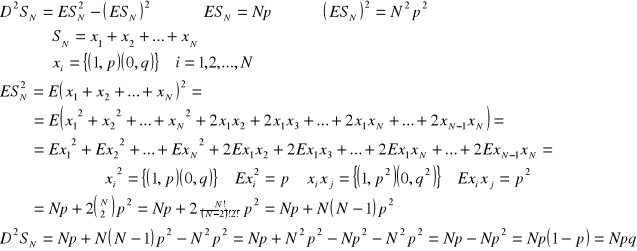
c.n.d.
43. Wektor, działania, długość, iloczyn skalarny, iloczyn wektorowy, prostopadłość, równoległość, krzywa stopnia drugiego
Wektor zaczepiony ![]()
to uporządkowana para punktów, gdzie A jest początkiem a B końcem
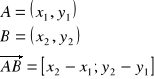
Wektor swobodny jest to rodzina równych wektorów zaczepionych.
Wektor zerowy ![]()
Wektor przeciwny do ![]()
to ![]()
, gdzie ![]()
Współrzędne wektora (w przestrzeni)
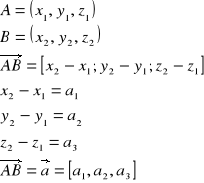
Długość wektora
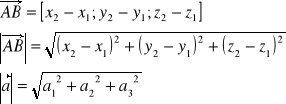
Równość wektorów
def.1.
Wektory są równe jeżeli są równoległe, mają ten sam zwrot i tą samą długość.
def.2.
Wektory są równe jeżeli ich odpowiednie współrzędne są równe
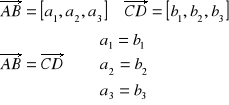
Własności równości wektorów:
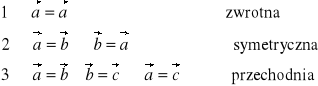
Suma wektorów
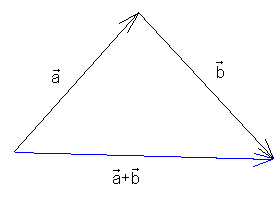
Sumą wektorów nazywamy wektor, którego początkiem jest początek pierwszego wektora, a końcem koniec ostatniego wektora.
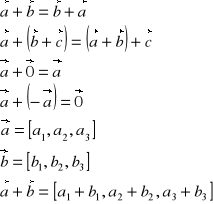
Różnica wektorów
Odejmowanie wektora ![]()
od wektora ![]()
jest równe sumie wektora ![]()
i wektora ![]()
przeciwnego do ![]()
.
![]()
Iloczyn wektora przez liczbę
Iloczynem wektora ![]()
przez liczbę m nazywamy wektor ![]()
mający długość ![]()
, kierunek ten sam co ![]()
i ten sam co ![]()
zwrot, gdy m>0 oraz zwrot przeciwny do ![]()
gdy m<0.
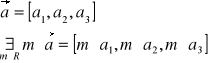
Iloczyn skalarny wektorów
def.1.
![]()
def.2.
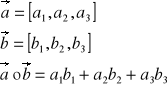
Iloczyn wektorowy wektorów
Jest wykonalny tylko w przestrzeni trójwymiarowej. Wektor będący wynikiem mnożenia jest prostopadły do obu czynników.
![]()
Równoległość wektorów
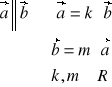
Prostopadłość wektorów
![]()
44. Prosta, równania, proste równoległe, proste prostopadłe, odległość punktu od prostej, odległość prostych równoległych.
Postać kierunkowa prostej
y=ax+b
Postać ogólna prostej
Ax+By+C=0
Postać odcinkowa prostej
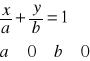
Równanie prostej przechodzącej przez dwa punkty
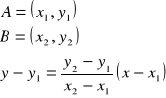
Proste równoległe
![]()
![]()
Proste prostopadłe
![]()
![]()
Odległość punktu od prostej
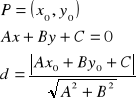
Odległość prostych równoległych
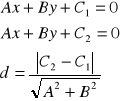
45. Okrąg, równania - wyprowadzanie
Równanie okręgu o środku w punkcie S=(a,b) i promieniu r:
![]()
wyprowadzenie:
|MN|=y
|NO|=x
|MO|=r
z ∆MNO z tw. Pitagorasa
![]()
Aby otrzymać równanie okręgu o środku w punkcie S=(a,b), należy początkowy okrąg przesunąć o wektor [a,b]. Punkty (x',y') przesuniętego okręgu spełniają warunek:
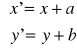
lub 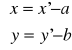
![]()
czyli
![]()
46. Zasada indukcji matematycznej, twierdzenia i zastosowanie
tw.
Jeżeli jakieś twierdzenie T(n) , w którym jest mowa o liczbie naturalnej jest prawdziwe dla liczby naturalnej n0 i jeżeli dla każdej liczby naturalnej ![]()
prawdziwa jest implikacja ![]()
, to twierdzenie T(n) jest prawdziwe dla każdej liczby naturalnej ![]()
.
Schemat dowodu metodą indukcji matematycznej:
I.
Sprawdzenie prawdziwości wzoru dla np. n=1 i n=2.
II.
Ułożenie założenia indukcyjnego (że dowodzone twierdzenie jest prawdziwe dla n=k)
III.
Postawienie tezy indukcyjnej (będzie udowadniane, że wzór jest prawdziwy dla wyrazu następnego czyli n=k+1, przy założeniu prawdziwości twierdzenia dla n=k).
IV.
Dowód.
Przykłady dowodów przeprowadzonych metodą indukcji matematycznej
47. Całka nieoznaczona, definicja, własności
W rachunku różniczkowym dla danej funkcji f(x) wyznaczało się f`(x). W rachunku całkowym wyznaczamy funkcję F(x), dla której znamy F'(x) tzn. wiadomo, że F'(x) = f(x), gdzie dane mamy f(x), a znaleźć należy F(x)
def. 1. funkcja pierwotna:
Funkcję pierwotną danej funkcji rzeczywistej f(x) w przedziale (a,b) nazywamy taką funkcję F(x), która ma własność:
F'(x) = f(x) dla ![]()
Przykład:
f(x) = cosx
![]()
ma funkcję pierwotną F(x) = sinx gdzie ![]()
bo F'(x) = cosx = f(x) dla ![]()
tw. 1.
Jeżeli f(x) ma w przedziale (a,b) funkcję pierwotną F(x) to f(x) ma w tym przedziale nieskończenie wiele tych funkcji pierwotnych. Każda z nich ma postać:
G(x) = F(x) + C, gdzie C jest dowolną stałą
Dowód:
W dowodzie wykażemy, że:
Dla danej funkcji pierwotnej F(x) funkcja G(x) = F(x) +C, C = const, jest funkcją pierwotną funkcji f(x)
Każdą funkcję pierwotną H(x) funkcji f(x) można uzależnić od tej danej F(x) i ta zależność ma postać H(x) = F(x) + C, gdzie C = const
dot. pierwszego:
Z założenia twierdzenia wiadomo, że F(x) jest funkcją pierwotną dla f(x) w przedziale (a,b) tzn. F'(x) = f(x) w (a,b).
Weźmy G(x) = F(x) + C, C = const.
Wówczas G'(x) = [F(x) + C]' = F'(x) = f(x) dla ![]()
Czyli G(x) spełnia warunki definicji funkcji pierwotnej dla f(x)
dot. drugiego:
Weźmy dwie funkcje pierwotne dla f(x) w przedziale (a,b) daną F(x) i inna H(x)
tzn F'(x) = f(x) dla ![]()
H'(x) = f(x) dla ![]()
Zatem F'(x) - H'(x) = 0 dla ![]()
Zatem [F(x) - H(x)]' = 0 dla ![]()
Więc F(x) - H(x) + C, C = const
Czyli H(x) = F(x) + ![]()
, gdzie ![]()
= C (![]()
- stałą dowolna)
Tzn. każdą funkcję pierwotną H(x) funkcji f(x) można przedstawić w postaci F(x) + C, C = const, a F(x) jest wyróżnioną funkcją pierwotną.
def. 2. całka nieoznaczona
Całką nieoznaczoną danej funkcji f(x) w przedziale (a,b) nazywamy zbiór wszystkich jej funkcji pierwotnych.
Całkę nieoznaczoną zapisujemy symbolem![]()
Zatem ![]()
= F(x) + C, gdzie F(x) jest funkcją pierwotną funkcji f(x), czyli F'(x) = f(x) dla ![]()
zaś C - dowolna stała
![]()
= F(x) +C ![]()
F'(x) = f(x) , C=const
UWAGA! F(x) + C, C = const przedstawia rodzinę funkcji
tw. 2.:
Każda funkcja f(x) ciągła w przedziale (a,b) ma swoją funkcję pierwotną F(x) a więc ma swoją całkę nieoznaczoną w przedziale (a,b)
podstawowe wzory:
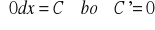
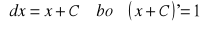
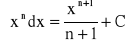
dla dowolnej liczby rzeczywistej n
-1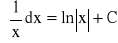
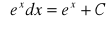
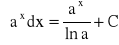
dla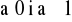
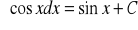
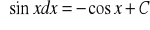
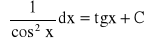
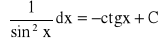
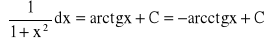
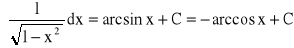
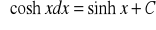
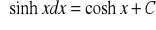
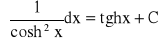
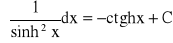
Własności całki nieoznaczonej:
Jeżeli istnieje całka
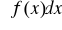
, to (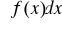
)' = f(x)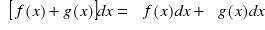
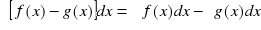
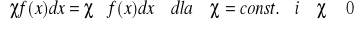
48. Całka oznaczona, definicje, własności, zastosowanie.
def.
Wiemy, że jeżeli F(x) jest funkcją pierwotną funkcji f(x) ciągłej w pewnym przedziale, to każda funkcja pierwotna funkcji f(x) w tym przedziale ma postać F(x) + C, gdzie C jest stałą. Wynika stąd, że różnica
F(x2) - F(x1)
w punktach x2 i x1 rozpatrywanego obszaru jest taka sama dla każdej funkcji pierwotnej F funkcji f. Różnicę tę nazywamy całką oznaczoną funkcji f od x1 do x2 i oznaczamy symbolem
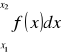
[A]
Mamy więc dla każdej funkcji f ciągłej w przedziale ![]()
:
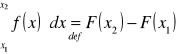
[B]
co zapisujemy także
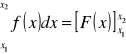
lub ![]()
i czytamy: całka oznaczona funkcji f(x) dx w granicach od x1 do x2 równa się F(x) z podstawieniem górnym x2 i dolnym xi.
Dokładna definicja całki oznaczonej jest bardziej rozbudowana:
Weźmy pod uwagę funkcję f(x), o której będziemy stale zakładali, że jest ograniczona w przedziale domkniętym ![]()
, tzn. dla ![]()
.
Dokonajmy różnych podziałów P1, P2,..., Pm, ... przedziału ![]()
na części. Niech podział Pm będzie osiągnięty przy pomocy nm - 1 liczb ![]()
, przy czym
![]()
,
gdzie dla ułatwienia oznaczyliśmy liczbę a jako ![]()
, a liczbę b jako ![]()
. Będziemy nazywali przedziały ![]()
, gdzie ![]()
, przedziałami cząstkowymi podziału ![]()
, a ich długości ![]()
oznaczali przez ![]()
. Niech ![]()
oznacza największą z liczb ![]()
, czyli długość najdłuższego przedziału cząstkowego podziału ![]()
. Ciąg podziałów ![]()
nazywamy normalnym ciągiem podziałów, jeżeli ![]()
.
Utwórzmy sumę ![]()
iloczynów wartości funkcji ![]()
w dowolnym punkcie ![]()
przedziału ![]()
przez długości ![]()
tych przedziałów przy podziale ![]()
:
![]()
[C]
Jeżeli ciąg ![]()
dla ![]()
jest zbieżny i do tej samej granicy przy każdym normalnym ciągu podziałów ![]()
niezależnie od wyboru punktów ![]()
, to funkcję ![]()
nazywamy funkcją całkowalną w przedziale ![]()
, a granicę ciągu [C] nazywamy całką oznaczoną funkcji![]()
w granicach od a do b i oznaczamy symbolem
[D]
Można wykazać, że jeżeli przy jakimś ciągu normalnym podziałów ciąg ![]()
ma granicę niezależną od wyboru punktów ![]()
, to funkcja ![]()
jest całkowalna.
Jednym z prostych sposobów tworzenia ciągu normalnego podziałów jest kolejne przepoławianie przedziałów cząstkowych; wówczas
![]()
, ![]()
.
Można również wykazać, że funkcja ciągła w przedziale domkniętym jest całkowalna, a nawet ogólniej, że funkcja ograniczona w przedziale domkniętym oraz ciągła w nim z wyjątkiem co najwyżej skończonej liczby punktów jest całkowalna.
Interpretacja geometryczna całki oznaczonej
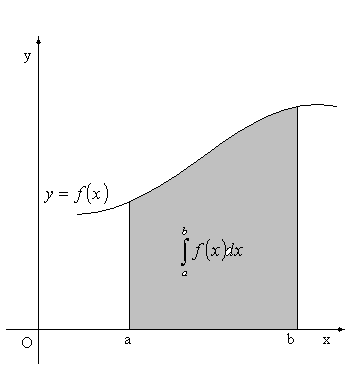
Jeżeli w przedziale ![]()
jest ![]()
, to pole obszaru ograniczonego łukiem krzywej ![]()
, odcinkiem osi Ox oraz prostymi x = a i
x = b równa się całce oznaczonej
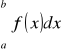
Jeżeli zaś w przedziale ![]()
jest ![]()
, to analogiczne pole równa się
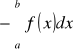
Zawsze więc pole wyżej określonego obszaru można wyrazić całką oznaczoną
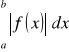
Przez 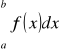
, gdzie a > b, rozumiemy całkę 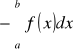
.
Przyjmujemy również, że 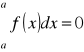
Własności całki oznaczonej
Addytywność całek oznaczonych względem przedziału całkowania.
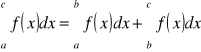
[E]
Stały czynnik można wyłączyć przed znak całki oznaczonej.
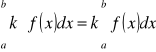
[F]
W szczególności, gdy k = -1
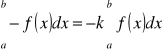
Całka sumy równa się sumie całek.
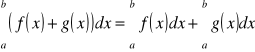
[G]
Jest to tzw. addytywność całki względem funkcji podcałkowej.
Całka oznaczona posiada więc własność tzw. liniowości ( własność 2. i 3.). Wzory powyższe należy rozumieć w ten sposób, że z istnienia całek po prawej stronie wynika istnienie całki po lewej stronie oraz podana równość.
Prawdziwy jest wzór:
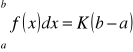
[H]
gdzie K jest pewną liczbą, spełniającą nierówność ![]()
, przy czym m oznacza kres dolny, a M kres górny funkcji f(x) w przedziale ![]()
.
Na podstawie własności Darboux mówiącej, że funkcja ciągła przybiera wszystkie wartości pośrednie między swymi kresami górnym i dolnym, wzór ten może przyjąć postać
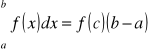
[I]
gdzie c jest pewną liczbą, spełniającą nierówność ![]()
, jeżeli funkcja podcałkowa f(x) jest ciągła w przedziale ![]()
.
Całka jako funkcja górnej granicy.
Jeżeli funkcja f(t) jest ciągła w przedziale![]()
, to funkcja
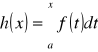
[J]
jest ciągła i różniczkowalna względem zmiennej x w przedziale ![]()
i w każdym punkcie tego przedziału zachodzi związek
![]()
[K]
Związek między całką oznaczoną a nieoznaczoną.
Jeżeli przez F(x) oznaczymy funkcję pierwotną funkcji f(x), ciągłej w przedziale ![]()
, tzn. jeżeli ![]()
, to ma miejsce wzór
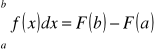
, [L]
przy czym oczywiście różnica ![]()
nie zależy od stałej całkowania C.
Wzór [L] nazywamy wzorem Leibniza-Newtona.
Uwaga. Prawą stronę powyższego wzoru oznacza się symbolem
![]()
lub ![]()
[M]
Całkowanie przez części dla całek oznaczonych.
Jeżeli u, v są funkcjami zmiennej x mającymi ciągłą pochodną, to
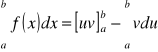
[N]
Jest to wzór na całkowanie przez części dla całek oznaczonych.
Całkowanie przez podstawienie dla całek oznaczonych.
Jeżeli g'(x) jest funkcją ciągłą, g(x) funkcją rosnącą w przedziale ![]()
, a f(u) funkcją ciągłą w przedziale ![]()
, to zachodzi następujący wzór:
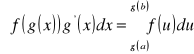
[O]
Jest to wzór na całkowanie przez podstawienie dla całek oznaczonych.
Jeżeli funkcja g różni się od funkcji h, całkowalnej na odcinku
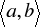
, tylko dla skończenie wielu argumentów z tego przedziału, to funkcja g również jest całkowalna i
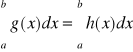
[P]
Wnioski:
1°. Funkcja nieciągła tylko dla skończenie wielu punktów przedziału![]()
i ograniczona w tym przedziale jest na nim całkowalna.
2°. Dla całkowalności funkcji ograniczonej w przedziale nie są istotne ani jej wartości, ani nawet określoność w końcach tego przedziału.
3°. Funkcja nieograniczona nie jest całkowalna (uwaga ta nie dotyczy tzw. całki niewłaściwej).
Znajdowanie długości łuku krzywej
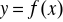
w przedziale
.
długość 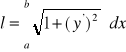
gdzie ![]()
[R]
Dla krzywej danej w postaci parametrycznej x = x(t), y = y(t), ![]()
mamy:
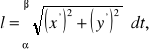
gdzie ![]()
![]()
[S]
Interpretacja fizyczna:
1°. Wiemy, że prędkość v(t) punktu P poruszającego się po osi OS jest pochodną drogi s(t) względem czasu t.
Droga S(t) jest więc funkcją pierwotną prędkości; stąd
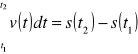
2°. Praca jako całka siły. Niech f(s) oznacza miarę na osi OS wektora siły działającej na masę umieszczoną w punkcie o współrzędnej s. Praca wykonana przez tę siłę na przesunięcie masy z położenia ![]()
w położenie ![]()
, równa jest całce funkcji f(s) od ![]()
do ![]()
.
praca 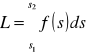
C
γ
b a
R
O
β
B
α c
A α
C'
B
β
c a
γ
C
α
A b
B
q
D
h p
C A
D
z
G
z y
r C
H
r
O y
u r
F
r
A
x
u
E
x
B
α
δ
γ
2β
2α
β
A
O B
r
C
β
δ γ
O
α
δ
A γ
B
C
O
A
B
C
E
F
O
A
D B
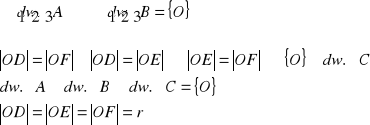
A
D
b c
C a B
a b
f1 f2
b c
a
c
f5
a c
f4 c
f3 b
b a
C
B' A'
O
A C' A” B
figura A figura B
1 2 4
h h h
3
a a a
są przystające
są przystające
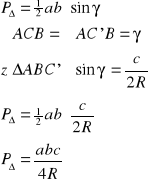
![]()
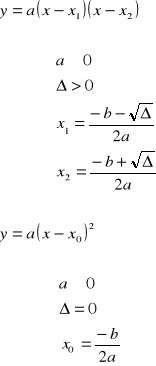
ć
ć
ć
ć


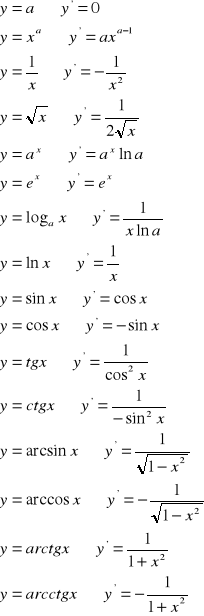
Wyszukiwarka
Podobne podstrony:
TM od 1 do 25, Definicje i twierdzenia na ustny egzamin maturalny z matematyki
USTNA97M, Zakres wymaga˙ na ustny egzamin maturalny z matematyki - technikum 5-letnie - maj 1996
Odpowiedzi na ustny egzamin z przedsiębiorczości
pytania na ustny[1], Egzamin specjalizacja ginekologia i położnictwo
ZESTAW TEMATOW NA WEWNETRZNY EGZAMIN MATURALNY Z JEZYKA POLSKIEGO W ZESPOLE SZKOL TECHNICZNYCH IM
USTNY EGZAMIN MATURALNY Z MATEMATYKI, szkoła, Matura, Matura - Matematyka, Zadania maturalne
Prezentacja maturalna, Ustny egzamin dojrzałości z języka polskiego, Jakub Żyła
Zestaw maturalny 2 Ustny Egzaminujący
Zestaw maturalny 6 Ustny Egzaminujący
probny egzamin maturalny z matematyki bydgoszcz luty 2013
Arkusz maturalny z matematyki na poziomie podstawowym rozwiazania
ZESTAWY PONIEDZIALEK, EGZAMIN Z CHORÓB PŁUC, zestawy na ustny
460-470, materiały ŚUM, IV rok, Patomorfologia, egzamin, opracowanie 700 pytan na ustny
Zaktualizowane pytania na egzamin ustny, egzamin na rzeczoznawcę majątkowego
584-606, materiały ŚUM, IV rok, Patomorfologia, egzamin, opracowanie 700 pytan na ustny
Co uczeń powinien wiedzieć o egzaminie z matematyki., Matura, Matematyka
283-317, materiały ŚUM, IV rok, Patomorfologia, egzamin, opracowanie 700 pytan na ustny
więcej podobnych podstron