SPRAWOZDANIE Z ĆWICZEŃ LABORATORYJNYCH Z MECHANIKI.

Temat: Wyznaczanie środka uderzenia oraz reakcji dynamicznych wahadła fizycznego w czasie uderzenia.

1.Cel ćwiczenia.

Celem ćwiczenia było wyznaczenie następujących wielkości:

- współczynnika restytucji dla materiałów wahadła,

- środka uderzenia wahadła,

- impulsu reakcji łożyska, w którym zamocowane jest wahadło.

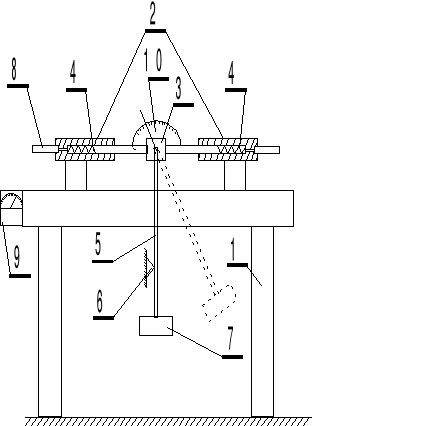
2. Schemat stanowiska pomiarowego:

a) stanowisko pomiarowe:

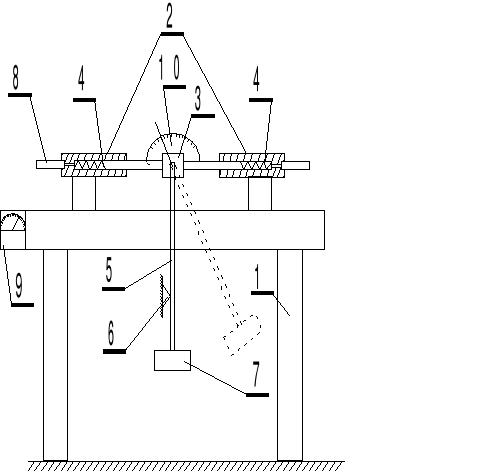
1- podstawa 2 - prowadnice 3 - tuleja 4 - sprężyny 5 - wahadło 6 - podpora 7 - masa 8 - czujnik przemieszczeń 9 - miernik siły 10 - kątomierz

Na podstawie zamocowane zostały prowadnice, które z kolei połączone zostały z tuleją przesuwną. Do tulei tej zamocowane jest wahadło. Do wyznaczenia wartości siły działającej na oprawkę w chwili uderzenia wahadła o podporę zastosowano dwie sprężyny o jednakowej sztywności. W prowadnicy znajduje się czujnik z miernikiem siły. Wahadło składa się z okrągłego pręta. Do podstawy zamocowany jest kątomierz służący do pomiaru kąta wychylenia wahadła z położenia równowagi. W czasie uderzenia w łożysku wahadła powstaje reakcja powodująca przemieszczenie oprawki, która oddziaływuje na czujnik przemieszczeń.

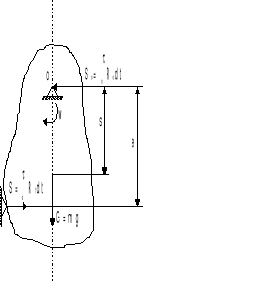
b) Układ sił działających na wahadło w chwili uderzenia:

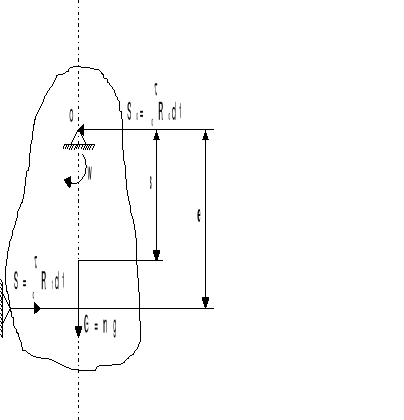
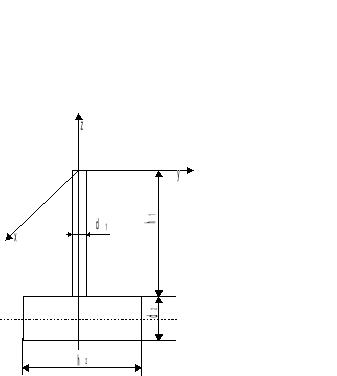
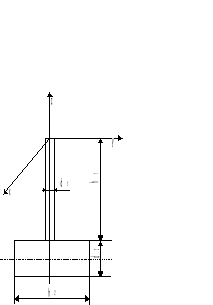
c) Schemat wahadła fizycznego:

2. Przebieg ćwiczenia.

a) Wyznaczanie współczynnika restytucji:

gdzie:

cosα - kąt przed uderzeniem;

cosα' - kąt wychylenia po uderzeniu.

Pomiar kątów wykonujemy pięciokrotnie i wyznaczamy wartości średnie :

Lp	α w stopniach	α' w stopniach
1	26	9
2	24	6
3	25	7
4	26	8
5	24	10
α = 25	α' = 8

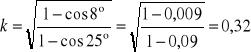
b) Wyznaczenie środka uderzenia wahadła.

Teoretyczny środek uderzenia wahadła wyznaczamy z zależności:

Doświadczalny środek uderzenia wahadła : e = 0,5 [m]

gdzie:

- impuls siły So = 0

- masowy moment bezwładności całego wahadła :

Ix = Ixc₁ + Ixc₂ = 0,0685+2,38 = 2,44 [kgm²]

- masowy moment bezwładności walca 1

Ixc₁= Ix₁ + md² = Ix₁ + m₁(h²₁/2) = 2,15⋅10 ^-4 + 0,068 = 0,0685 [kgm²]

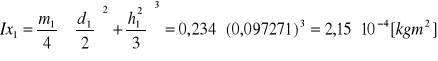
- masowy moment bezwładności walca 2

Ixc₂= Ix₂ + m₂+(h₁+d₂/2)² = 2,38⋅10 ^-6 + 2,38 = 2,38 [kgm²]

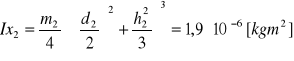
- masa całego wahadła:

Wahadło wykonane zostało ze stali. Gęstość stali wynosi ς = 7,8 ⋅ 10 ³ kg/m³. Masę wahadła wyznaczamy z zależności m = v⋅ς

Objętość walców 1,2 :

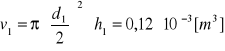
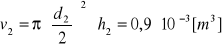
Masy walców 1,2 :

Zatem masa całkowita wahadła :

m_c = m₁ + m₂ = 7,96 [kg]

Wyznaczenie odległości środka masy od osi obrotu :

x_c = 0 z_c = 0 y_c = S

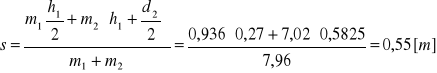
c) Wyznaczanie impulsu siły w łożyskach:

So = (1+k)mϖ[i²/e-s]

gdzie:

e = 0,55m

i² = es = 0,55m ⋅ 0,55m = 0,30m²

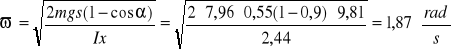
So = (1+0,32) ⋅ 7,96 ⋅ 1,87[0,30/0,55-0,55] = 1,32 ⋅ 7,96 ⋅ 1,87(-0,004) = 0,08 [Ns]

3.Wnioski.

Wyznaczona wartość teoretyczna ramienia działania impulsu względem osi obrotu - e, różni się od doświadczalnie wyznaczonej z powodu dużej niedokładności : przyrządów pomiarowych, odczytu wskazań kątomierza wychyleń wahadła.

---