Ćwiczenie 6 „OPÓR”

Temat: Termiczny współczynnik oporu przewodnika.

Cel: Badanie zależności oporu przewodnika od temperatury. Wyznaczenie termicznego współczynnika oporu przewodnika.

Przyrządy: Łaźnia wodna, naczynie z opornikiem, mostek Wheatstone'a, cyfrowy miernik temperatury, regulator mocy.

Literatura: R. Resnick, D. Halliday, FIZYKA, t. II, § 31-1 do 31-4,

D. Halliday, R. Resnick, J. Walker, PODSTAWY FIZYKI, t. 3., § 27.4 do 27.6

I. Metoda pomiaru.

Teoretyczne modele przewodnictwa elektrycznego metalu zweryfikowane doświadczalnie wskazują, że w temperaturach od ok. 300 K do ok. 800 K opór jest proporcjonalny do pierwszej potęgi temperatury bezwzględnej. Inaczej mówiąc, opór elektryczny metalu jest liniową funkcją temperatury dla temperatur kilkuset kelwinów. Stosując praktyczną skalę temperatur w stopniach Celsiusza zależność tę można zapisać

(1)

R₀ - opór przewodnika w temperaturze 0⁰C, α - temperaturowy współczynnik oporu,

t - temperatura w skali Celsjusza .

Niniejsze ćwiczenie może posłużyć sprawdzeniu tego prawa. W tym celu korzystamy z układu pomiarowego przedstawionego na rys 1, który składa się z mostka Wheatstone'a (3) do pomiaru oporu elektrycznego, naczynia zawierającego badany przewodnik zanurzony w kąpieli olejowej (2), termometru elektrycznego (4), łaźni wodnej (1) służącej do podgrzewania naczynia z badanym opornikiem i autotransformatorem (5) do zasilania grzałki łaźni wodnej,

Rys. 1. Schemat układu pomiarowego

Po zmontowaniu układu pomiarowego dokonujemy równoczesnego pomiaru oporu przewodnika i temperatury. Zarówno opór jak i temperatura w sposób płynny zmieniają się podczas ogrzewania. Pomiar oporu za pomocą mostka wymaga chwili czasu na jego zrównoważenie. Dlatego znając tendencję zmian oporu podczas ogrzewania wygodnie jest z wyprzedzeniem ustawić na mostku opór i odczytać temperaturę w chwili gdy mostek będzie w równowadze lub mierzyć opór w chwili gdy układ osiągnie wybraną temperaturę. Do pomiarów zależności R(t) nie jest konieczna stała zmiana temperatury. Pomiaru dokonujemy w zakresie temperatur od pokojowej do max. 85^o C. W oparciu o wykonane pomiary dopasowujemy korzystając z metody najmniejszych kwadratów analityczną postać linii prostej:

R(t) =A·t + B (2)

Znając wartości współczynników A i B prostej i porównując je ze współczynnikami równania (2) otrzymujemy wzory:

A = R₀ α i B = R₀ (3)

z których wynika, że temperaturowy współczynnik oporu wynosi:

α = A/B (4)

2. Zasada działania mostka Wheatstone'a

Do pomiaru oporu elektrycznego używany jest układ mostkowy przedstawiony na rysunku 2, gdzie R₁, R ₂ , R ₃ oznaczają znane wartości oporów, które można dowolnie zmieniać. Natomiast R_x oznacza szukany opór. Zasada pomiaru polega na takim doborze wartości oporów: R₁, R ₂ , R ₃, aby przez galwanometr G prąd nie płynął. Taki stan układu nazywamy zrównoważeniem mostka. Galwanometrem w tym układzie jest wbudowany czuły amperomierz. Opory R₁ i R₂ są fabrycznie ustalone, a R₃ można zmieniać w sposób płynny.

Na podstawie praw Kirrchoffa można zapisać następujące równania:

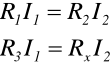
(5)

Z tego układu równań otrzymujemy wzór

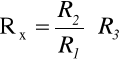
(6)

który pozwala wyznaczyć szukany opór.

Ta metoda pomiaru jest bardzo dokładna gdyż pomiar dokonuje się za pomocą przyrządu przez, który nie płynie prąd i nie ma zakłóceń mierzonych wielkości. Taką metodę pomiaru nazywamy kompensacyjną.

3. Wykonanie i opracowanie ćwiczenia.

UWAGA! Szczegółowy przebieg wykonania ćwiczenia określa osoba prowadząca.

1. Połączyć obwód w/g schematu ideowego (rys. 1).

2. Regulatorem mocy 5 podgrzać wodę maksymalnie do temperatury 85°C. Odczekać ok. 5 minut, po czym zbiorniczek z badanym opornikiem wyjąć z wody unosząc odpowiednie ramię statywu do góry. Przykryć łaźnię wodną pokrywą.

3. Mierzyć opór przewodnika wraz ze opadającą temperaturą co dwa stopnie, aż do osiągnięcia temperatury bliskiej temperaturze otoczenia. Zanotować wyniki w tabeli:

t [oC]
R [Ω]

1. Nanieść na wykres R = f(t) punkty pomiarowe zamieszczone w tabeli.

2. Wyznaczyć analityczną zależność oporu elektrycznego przewodnika od temperatury korzystając z metody najmniejszych kwadratów:

3. Na podstawie uzyskanych wyników narysować zależność R(t) oraz nanieść prostokąty niedokładności punktów pomiarowych. Przykładowy wykres przedstawia rys. 3.

Rys. 3.

6. Korzystając z wyznaczonych metodą najmniejszych kwadratów wartości współczynników A i B i ich niepewności u(A) i u(B), obliczyć na podstawie wzoru [1] wartość temperaturowego współczynnika oporu elektrycznego α i jego niepewność pomiarową u_c(α) korzystając ze wzoru:

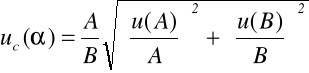
(7)

IV. Wnioski

1. Podać w poprawnej formie otrzymane wyniki wraz z odpowiednimi niepewnościami (α ± u_c(α)).

2. Określić źródła niepewności i przyczyny rozbieżności położeń punktów pomiarowych od linii prostej.

V. Pytania kontrolne.

1. Jaki rodzaj wiązań krystalicznych występuje w metalach?

2. Co to jest prąd elektryczny i jego mechanizm przepływu?

3. Przyczyny zmian oporu przewodnika wraz ze zmianą temperatury.

4. Co to jest opór elektryczny i w jakich jednostkach się go mierzy?

5. Wyjaśnij prawa Ohma

1. Zasada działania mostka Wheatstone'a.

2. Omówić metodę wyznaczania temperaturowego współczynnika oporu stosowaną w ćwiczeniu.

x

R

3

R

1

I

1

R

1

I



Rys. 1. Schemat mostka Wheatstone'a.

2

R

2

I

G

R[Ω]

t[^oC]

---