Szeregi liczbowe

Niech
będzie dowolnym ciągiem liczb rzeczywistych.

Definicja

Szeregiem liczbowym o wyrazach
nazywamy ciąg
, zwany ciągiem sum częściowych, gdzie

dla

Szereg oznaczamy

Szereg nazywamy zbieżnym, jeżeli ciąg sum częściowych
jest zbieżny.

Jeżeli

,

to liczbę S nazywamy sumą szeregu, piszemy
.

Szereg nazywamy rozbieżnym, jeżeli nie jest zbieżny.

Jeżeli ciąg sum częściowych jest rozbieżny do
, to mówimy, że szereg jest rozbieżny do
i piszemy
.

Szereg nazywamy bezwzględnie zbieżnym, jeżeli szereg
jest zbieżny.

Szereg zbieżny nazywamy warunkowo zbieżnym, gdy szereg
jest rozbieżny.

czyli szereg warunkowo zbieżny jest zbieżny, ale nie jest bezwzględnie zbieżny.

Tw. (warunek konieczny zbieżności szeregu)

Jeżeli szereg
jest zbieżny, to
.

Wniosek

Jeżeli
, to szereg
jest rozbieżny.

Tw. (warunek Cauchy'ego zbieżności szeregu)

Szereg
jest zbieżny wtedy i tylko wtedy, gdy

WAŻNE SZEREGI

Szereg geometryczny

Szereg geometryczny o ilorazie bezwzględnie mniejszym od 1 jest zbieżny.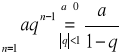

Szereg harmoniczny

Szereg harmoniczny jest rozbieżny, a ciąg jego sum częściowych rośnie do
.

Szereg harmoniczny rzędu r , (uogólnony szereg harmoniczny z wykładnikiem r)

Szereg
jest zbieżny wtedy i tylko wtedy, gdy
.

Dla
szereg
jest rozbieżny.

Szereg anharmoniczny

Szereg anharmoniczny jest zbieżny.

Tw. działania na szeregach

Jeżeli szeregi
,
są zbieżne, to

a) szeregi
są zbieżne oraz

b) szereg
,
jest zbieżny

Kryteria zbieżności szeregów

Szeregi o wyrazach nieujemnych

TW .

Jeżeli ciąg sum częściowych szeregu o wyrazach nieujemnych jest ograniczony z góry, to szereg jest zbieżny.

Tw. Kryterium porównawcze zbieżności szeregów

Jeżeli wyrazy szeregów
,
są nieujemne oraz dla prawie wszystkich liczb naturalnych spełniona jest nierówność
, to

1) jeżeli szereg
jest zbieżny, to szereg
jest zbieżny;

2) jeżeli szereg
jest rozbieżny, to szereg
jest rozbieżny.

Tw. Kryterium ilorazowe (d'Alamberta)

Jeżeli wyrazy szeregu
są dodatnie oraz
, to

dla
szereg jest zbieżny,

dla
szereg jest rozbieżny.

Tw. Kryterium pierwiastkowe (Cauchy'ego)

Jeżeli wyrazy szeregu
są nieujemne oraz
, to

dla
szereg jest zbieżny,

dla
szereg jest rozbieżny.

Uwaga

Kryterium Cauchy'ego jest silniejsze od kryterium d'Alamberta. Jeśli kryterium ilorazowe rozstrzyga o zbieżności szeregu, to i kryterium pierwiastkowe także rozstrzyga.

Szeregi o wyrazach dowolnych

Szereg postaci


nazywamy szeregiem naprzemiennym.

Wyrazy tego szeregu są naprzemian dodatnie i ujemne.

Tw. Kryterium Leibniza

Jeżeli ciąg
jest nierosnący oraz
, to szereg naprzemienny
jest zbieżny

oraz
.

Zbieżność bezwzględna i warunkowa

TW:

Jeżeli szereg
jest zbieżny, to szereg
jest zbieżny.

tzn.

Jeżeli szereg jest zbieżny bezwzględnie, to jest zbieżny.

Twierdzenie odwrotne nie zachodzi.

Uwaga!

Jeżeli szereg jest zbieżny bezwzględnie, to dowolna zmiana kolejności wyrazów lub łączenie wyrazów w grupy - nie narusza zbieżności szeregu ani nie zmienia jego sumy.

Jeżeli szereg jest warunkowo zbieżny, to zmieniając kolejność wyrazów można otrzymywać szeregi o różnych sumach lub szeregi rozbieżne.

Zadania zrobione na wykładzie

Zad.1 Z definicji zbadaj zbieżność szeregu a)
, b)

Odp.
,

Zad.2 Obliczyć sumę szeregu

Zad.3 Wykazać rozbieżność szeregu

Szereg rozbieżny gdyż nie spełnia warunku koniecznego zbieżności

zad.4 Zbadaj zbieżność szeregów z kryterium porównawczego
, b)

a) szereg rozbieżny, b) szereg zbieżny

zad.5 Zbadaj zbieżność szeregów

odp. szereg zbieżny z kryterium ilorazowego.

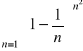
odp. szereg zbieżny z kryterium pierwiastkowego.

Zad.6 Wykazać, że szereg anharmoniczny spełnia kryterium Leibniza.

---