Wykład 5

Określenie różniczki, gradientu, wzór Taylora

Rozważmy funkcję f n zmiennych

,

która ma w punkcie
pochodne cząstkowe rzędu pierwszego. Niech
będzie wektorem z
takim, że
.

Definicja

Wyrażenie

nazywamy różniczką zupełną funkcji f w punkcie
i oznaczamy symbolem
.

Dla
różniczkę zupełną funkcji f w punkcie
zapiszemy

.

lub wprowadzając oznaczenia
,

Przykład

Wyznaczyć różniczkę zupełną funkcji
w punkcie (1,2).

Definicja

Gradientem funkcji f w punkcie
nazywamy wektor pochodnych cząstkowych

Dla

.

Różniczka jest iloczynem skalarnym wektorów

Definicja

Jeżeli funkcja f jest klasy
, to wyrażenie

nazywamy różniczka zupełną rzędu m funkcji f .

Dla

druga różniczka funkcji f dwóch zmiennych wyraża się wzorem

zapis macierzowy

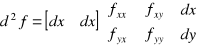
Z uwagi na to że funkcja f jest klasy
macierz drugich pochodnych cząstkowych jest symetryczna.

Trzecia różniczka funkcji f klasy
jest równa

Ze względu na podobieństwo prawej strony do wzoru dwumianowego Newtona stosujemy zapis symboliczny

Przykład

Obliczyć druga różniczkę funkcji

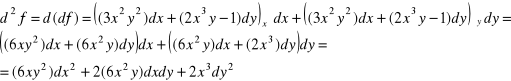
Niech

TW. (wzór Taylora )

Jeżeli funkcja f jest klasy
w otoczeniu U punktu
, to dla każdego punktu
istnieje taki punkt
,
, że

.

Wyrażenie

nazywamy wielomianem Taylora stopnia
.

Dla
,
,

gdzie
,
,
,
. Punkt
jest punktem odcinka o końcach
i
.

Przykład

Napisac wzór Taylora z trzecia resztą dla funkcji
w punkcie (1,-1).

Ekstremum funkcji

Załóżmy, że funkcja f n zmiennych jest określona w pewnym otoczeniu punktu
.

Definicja

Funkcja f ma w punkcie
minimum właściwe, jeżeli istnieje takie sąsiedztwo punktu
, że dla każdego punktu
należącego do tego sąsiedztwa spełniona jest nierówność

.

Funkcja f ma w punkcie
maksimum właściwe, jeżeli istnieje takie sąsiedztwo punktu
, że dla każdego punktu
należącego do tego sąsiedztwa spełniona jest nierówność

.

Jeżeli zamiast nierówności mocnej (>, < )zachodzi nierówność słaba(≥, ≤), to mówimy, że funkcja f ma w
minimum (maksimum).

Minima i maksima (właściwe lub niewłaściwe) nazywamy ekstremami. Ekstremum jest lokalną własnością funkcji, charakteryzuje rozkład wartości funkcji w dowolnie małym otoczeniu danego punktu. Nie należy mylić ekstremów lokalnych z ekstremami globalnymi (absolutnymi) czyli z wartością największą oraz wartością najmniejszą funkcji na zadanym zbiorze.

Przykład

Korzystając z definicji rozstrzygnąć, czy funkcja f ma we wskazanym punkcie ekstremum.

TW. Warunek konieczny istnienia ekstremum

.

Jeżeli funkcja f ma w punkcie
ekstremum i ma w tym punkcie pochodne cząstkowe rzędu pierwszego, to są one równe zero

dla
.

krótko
.

Dowód

Przypadek

Punkty, w których spełniony jest warunek

nazywamy punktami stacjonarnymi funkcji f.

Wniosek

Funkcja wielu zmiennych może mieć ekstremum jedynie w punktach stacjonarnych lub w punktach, w których nie istnieje przynajmniej jedna pochodna cząstkowa rzędu pierwszego.

Macierz drugich pochodnych cząstkowych

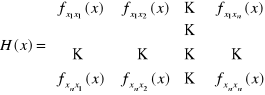
nazywamy macierzą Hessego.

Jeżeli funkcja f jest klasy C² w pewnym zbiorze, to macierz Hessego dla punktów z tego zbioru jest macierzą symetryczną (tw. Schwarza, pochodne mieszane są wówczas równe).

8

---