Wykład 2: Wzory i własności wykorzystywane przy obliczaniu prawdopodobieństwa

1. Prawdopodobieństwo warunkowe.

Prawdopodobieństwo warunkowe to podstawowe pojęcie teorii prawdopodobieństwa. W zasadzie każde zadanie z rachunku prawdopodobieństwa da się zapisać przy użyciu prawdopodobieństwa warunkowego.

Elementarny przykład

Wyobraźmy sobie, że mamy dwie urny. W pierwszej są same białe kule, w drugiej same czarne. Najpierw wybieramy losowo urnę, a później losujemy kolejno dwie kule. Niech A oznacza zdarzenie, że pierwsza kula jest biała. B oznacza zdarzenie, że druga kula jest biała.

, bo wybór urny determinuje wybór koloru kuli. Jeśli wiemy, że zaszło zdarzenie A, to druga wylosowana kula będzie biała, więc prawdopodobieństwo zajścia zdarzenia B, gdy wiemy, że zaszło zdarzenie A oznaczane przez

P(B | A)

jest równe 1.

Definicja

Prawdopodobieństwem warunkowym zajścia zdarzenia A pod warunkiem zajścia zdarzenia B, gdzie P(B) > 0, nazywamy liczbę

(jest to iloraz prawdopodobieństwa części wspólnej zdarzeń A, B i prawdopodobieństwa zdarzenia B).

Zadanie

Rzucamy trzema kostkami. Jakie jest prawdopodobieństwo, że na żadnej kostce nie wypadła szóstka, jeśli na każdej kostce wypadła inna liczba oczek?

Niech A oznacza zdarzenie, że nie wypadła szóstka.

B - zdarzenie, że na każdej kostce wypadła inna liczba oczek.

Chcemy użyć wzoru z definicji.

,
. Stąd
.

Zdarzenia niezależne

Jeżeli zdarzenia A i B są niezależne

to P(A | B) = P(A).

2. Prawdopodobieństwo całkowite (zupełne).

Przykład: urna I - 3 białe, 5 czarnych, 2 zielone;

urna II - 4 białe, 1 czarna, 5 zielonych;

urna III - 1 biała, 2 czarne, 7 zielonych.

Rzucamy kostką do gry. Jeżeli wypadnie 1 oczko, to losujemy kulę z urny I; jeżeli wypadnie parzysta liczba oczek, to losujemy kulę z urny II; dla pozostałych wyników na kostce losujemy kulę z urny III. Jakie jest prawdopodobieństwo wylosowania kuli czarnej?

1. Wszystkie przypadki wyników na kostce (zdarzeń) A_i wykluczają się parami (są parami rozłączne),

2. Suma wszystkich zdarzeń A_i jest zdarzeniem pewnym,

3. P(A_i) > 0.

3. Prawdopodobieństwo przyczyny (wzór Bayesa).

Przykład: rzut kostką i losowanie kuli jak wyżej. Wiemy, że wylosowaliśmy kulę białą. Jakie jest prawdopodobieństwo wylosowania kuli białej z urny II?

4. Schemat Bernoulliego (próby, proces Bernoulliego)

Bernoulli to nazwisko słynnej rodziny szwajcarskich matematyków.

Nicolas Bernoulli (1623-1708)

x Margaretha N...

│

├──> Jakob Bernoulli (1654-1705)

│

├──> Nicolas Bernoulli (1662-1716)

│ x N...

│ │

│ └──> Nicolas Bernoulli (1687-1759) alias Nicolas I

│

└──> Johann Bernoulli (1667-1748) alias Johann I

x Dorothée Falkner

│

├──> Nicolas Bernoulli (1695-1726) alias Nicolas II

│

├──> Anne Bernoulli (Anne Catherine) 1698-1784

│ x 1720 : Jean Dollfus

│ x apr. 1736 : Pierre Hammer

│

├──> Daniel Bernoulli (1700-1782)

│

└──> Johann Bernoulli (1710-1790) alias Johann II

x N...

│

├──> Johann Bernoulli (1744-1807) alias Johann III

│

├──> Daniel Bernoulli (daty nieznane)

│

└──> Jakob Bernoulli (1759-1789) alias Jakob II

Próba Bernoulliego - eksperyment losowy z dwoma możliwymi wynikami, określanymi zazwyczaj jako sukces (1) oraz porażka (0). Za przykłady prób Bernoulliego matematycy uważają:

• pojedynczy rzut monetą (rezultat: orzeł lub reszka)

• narodziny dziecka (rezultat: chłopiec lub dziewczynka).

Ciąg niezależnych prób Bernoulliego nazywa się procesem (schematem) Bernoulliego.

n : liczba niezależnych prób

k : liczba sukcesów, n - k : liczba porażek

p: prawdopodobieństwo sukcesu w pojedynczej próbie

q = 1 - p : prawdopodobieństwo porażki w pojedynczej
próbie

Jakie jest prawdopodobieństwo, iż na n wykonanych (niezależnych) prób uzyskamy dokładnie k sukcesów?

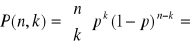
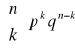
Rozkład dwumianowy (rozkład Bernoulliego)

---