Statystyka ćwiczenia
T: Analiza szeregu szczegółowego
Wartość średniej arytmetycznej
Wartość dominanty
Wartość środkową ( medianę )
Wartość rozstępu, warianty i odchylenie standardowe
Współczynnik zmienności
Odchylenie przeciętne i współczynnik zmienności
Dokonać analizy porównawczej poziomu inteligencji uczniów klasy IV dzieląc całą ich zbiorowość na dwie populacje, dziewcząt i chłopców od a do f
127K,129K,130K,132M,134M,135M,135M,135M,135M,140M,142M,143M,
143M,144M,145K145K,149K,152K,152M,153K
Populacja generalna - wszyscy uczniowie klas IV w danej miejscowości
Próba losowa
Próba reprezentacyjna
x - liczba punktów
n=20 - liczebność próby ( ![]()
- mała próba )
szereg szczegółowy - szereg uporządkowany badany bezpośrednio
127,129,130,132,134,135,135,135,135,140,142,143,143,144,145,145,149,152,152,153
a) Średnia arytmetyczna
![]()
![]()
- przeciętna liczba poziomu inteligencji w grupie 20 osobowej
b)
Dominanta ( moda, wartość najczęstsza ) - najczęściej występująca liczba
D=135
c)
Mediana - wartość cechy statystycznej dla której 50% elementów zbiorowości przyjmuje mniejsze od mediany, a 50% wartości większe od mediany. Dzieli badaną zbiorowość na dwie równe części pod względem liczebności
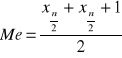
dla parzystej liczby n
![]()
dla nieparzystej liczby n
![]()
50% uczniów ma poziom inteligencji większy niż 141 a 50% mniejszy
Kwartyl 1 (Q1)
Szereg I - szereg od początku zbioru do środka wraz z medianą
Szereg II - mediana + szereg do końca zbioru
Q1=Me(szereg I) = 135
Q2=Me(szereg II) = 145
Q1 - oznacza, że 25% elementów zbiorowości ma poziom inteligencji mniejszy
lub równy 135, a 75% większy lub równy 135
Q2 - oznacza, że 75% elementów zbiorowości ma poziom inteligencji mniejszy
lub równy 145, a 25% większy lub równy 145
d)
miary rozstępu ( dyspersji )
wariancje
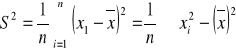
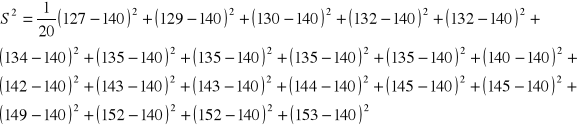
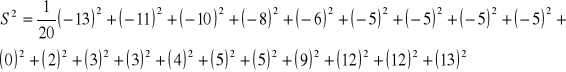
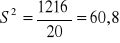
S2 - poszczególne elementy minus średnia arytmetyczna podniesione
do kwadratu, zsumowane i podzielone przez liczbę elementów
odchylenie standardowe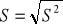
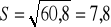
rozstęp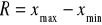
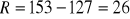
współczynnik zmienności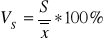
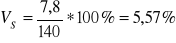
odchylenie przeciętne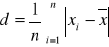
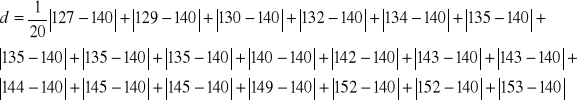
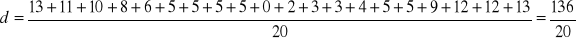
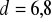
współczynnik zmienności
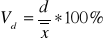
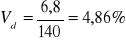
typowy obszar zmienności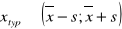
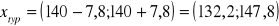
reguła trzech sigm
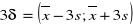
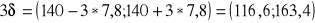
XD - średnia dla dziewcząt
XC - średnia dla chłopców
|
|
Dziewczęta |
Chłopcy |
|
Średnia |
141,25 |
127,25 |
|
Średnia arytmetyczna |
142 |
138 |
|
Dominanta |
145 |
135 |
|
Mediana |
145 |
137,50 |
|
Rozstęp |
26 |
20 |
|
Odchylenie standardowe |
10,16 |
5,70 |
|
Wariancja |
103,25 |
32,50 |
|
Współczynnik zmienności |
7,15% |
4,13% |
|
Odchylenie przeciętne |
9,25 |
4,25 |
|
Współczynnik zmienności |
6,51% |
3,07% |
![]()
![]()
![]()
![]()
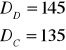
![]()
![]()
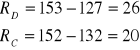
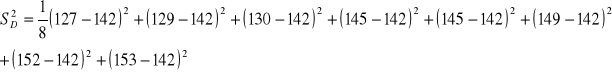
![]()
![]()
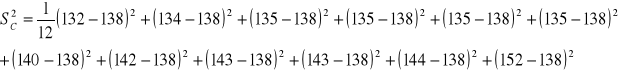
![]()
![]()
![]()
![]()
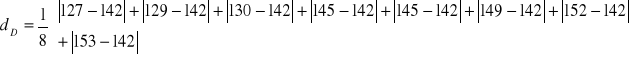
![]()
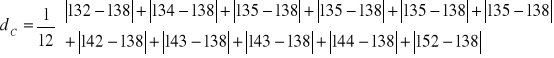
![]()
![]()
![]()
![]()
![]()
Interpretacja:
Przeciętny poziom inteligencji dziewcząt przewyższa o 4 punkty przeciętny poziom inteligencji chłopców
Wartości dominanty i mediany są wyższe w grupie dziewcząt. W tej grupie wiekowej tłumaczy się to szybszym rozwojem psychofizycznym niż chłopców
Rozstęp cechy w grupie chłopców jest mniejszy niż w grupie dziewcząt
co wpływa na wysokość wariancji, odchylenia standardowego oraz współczynnika zmiennościBardziej stabilna ze względu na poziom inteligencji jest grupa chłopców ( im mniejszy współczynnik zmienności tym większa stabilność )
Zadanie
W pewnym mieście zebrano informacje o liczbie osób zatrudnionych w małych firmach prywatnych.
Wielkości zatrudnienia w poszczególnych firmach są następujące:
n=40
1,1,2,2,3,4,5,5,6,6,6,7,7,7,7,8,9,9,10,10,12,12,12,12,13,14,14,14,15,15,15,15,15,15, 16, 18, 20, 23, 25, 30
Dokonać agregacji danych budując szereg rozdzielczy o jednakowej rozpiętości
a następnie przeanalizować szereg rozdzielczy:
przeciętne zatrudnienie w firmie
typowa liczba zatrudnionych w firmie
wyznaczyć medianę
określić stopień zróżnicowania poszczególnych elementów w całej zbiorowości
wykazać symetrię, bądź asymetrię
zbadać stopień skoncentrowania
k - liczba przedziałów klasowych.
Sposoby podziału
n
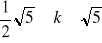
k |
|
30 - 60 |
6 - 8 |
60 - 100 |
5 - 10 |
niech k=6
b - długość przedziału klasowego ( rozpiętość )
![]()
![]()
|
Liczba |
Środki |
|
|
8 |
2,5 |
|
|
12 |
7,5 |
|
|
14 |
12,5 |
|
|
3 |
17,5 |
|
|
2 |
22,5 |
|
|
1 |
27,5 |
|
|
|
X |
410 |
a) x - liczba osób zatrudnionych ni - wagi
![]()
![]()
b) Dominanta ( szeregu rozdzielczego ) - wybieramy przedział zawierający największą liczbę elementów
![]()
D=10,77
|
8 20 34 37 39 40 |
c) Mediana - dolna granica w której znajduje się mediana
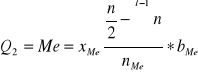
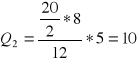
osób
5,6 - zajęcia - ćwiczenia
7,8 - zajęcia - test końcowy ( zadania samodzielne )
Miary tendencji centralnej
klasyczne
średnia arytmetyczna
średnia geometryczna
dominanta
Kwartyle ( Q1,Q2,Q3)
Kwintyle ( co 5 )
Dentyle ( co 10 )
Me
Suma liczebności wszystkich przedziałów poprzedzających przedział mediany
Wyszukiwarka
Podobne podstrony:
Materialy pomocnicze do cwiczen Statystyka cz I
Koncentracja - zadłużenie, semestr I, STATYSTYKA, ćwiczenia Plenikowska
Cwiczenie 4 Statystyczna obróbka wyników pomiarowych
Indeksy agregatowe, Statystyka - ćwiczenia - Rumiana Górska
WNIOSKOWANIE STATYSTYCZNE 12.10.2013, IV rok, Ćwiczenia, Wnioskowanie statystyczne
t, Statystyka, ćwiczenia
zadanie o analizie struktury, statystyka i demografia-Hnatyszyn-Dzikowska ćwiczenia
Statysta kolokwium ubiegly, Stosunki międzynarodowe - materiały, II semestr, Statystyka i demografia
ĆWICZENIE 501, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i
Ćwiczenie 1, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mullera i b
ĆWICZENIE 501LAST, MIBM WIP PW, fizyka 2, laborki fiza(2), 50-Charakterystyka licznika Geigera-Mulle
Analiza regresji, Statystyka - ćwiczenia - Rumiana Górska
WNIOSKOWANIE STATYSTYCZNE 26.10.2013, IV rok, Ćwiczenia, Wnioskowanie statystyczne
QUIZ 2 statystyka, WSFiZ Białystok - zarządzanie, Semestr II, Statystyka - ćwiczenia
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 01.06.2008
Statystyka Ćwiczenia (Teoria)
statystyka zadanie, statystyka i demografia-Hnatyszyn-Dzikowska ćwiczenia
Centralne Twierdzenie Graniczne, PSYCHOLOGIA, I ROK, semestr II, podstawy metodologii badań psycholo
calosc, WSFiZ, IV semestr, Statystyka (ćwiczenia)
więcej podobnych podstron