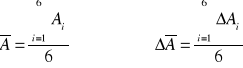Sprawozdanie z wykonania ćwiczenia nr 320.

TEMAT : POMIAR PRACY WYJŚCIA TERMOELEKTRONÓW.
IMIĘ I NAZWISKO : SEBASTIAN GOS
WYDZIAŁ : Elektryczny	SEMESTR : zimowy	ROK AKADEMICKI : 1999/2000
ZESPÓŁ : nr 7	DATA WYKONANIA : 13 grudnia 1999
OCENA :	PODPIS :

Prąd nasycenia I_n odpowiada całkowitemu strumieniowi elektronów emitowanych z katody, jest więc iloczynem gęstości j_n prądu emisyjnego i czynnej powierzchni
katody:

Przy pewnym określonym napięciu anodowym wysokość bariery potencjału staje się równa zeru; odpowiada to napięciu, przy którym wszystkie wyemitowane przez katodę elektrony dotrą do anody. Otrzymamy wtedy prąd nasycenia. Gęstość prądu nasycenia zależy od temperatury katody i wyraża się wzorem Richardsona:

gdzie:

B - stała

T - temperatura katody w kelwinach

A - praca wyjścia elektronu z katody

k- stała Boltzmana

Po uwzględnieniu prawa Richardsona otrzymamy:

W oparciu o prawo Richardsona można wyznaczyć pracę wyjścia elektronu. Zakładając, że znamy dwie wartości prądu nasycenia termoemisji
i
oraz odpowiadające tym prądom temperatury
i
możemy napisać:

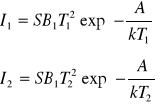
skąd

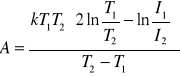
Do pomiaru pracy wyjścia wykorzystuje się diodę lampową z katodą wolframową ponieważ charakterystyka prądowo-napięciowa tej lampy wykazuje wyraźne nasycenie prądu anodowego. Aby z wyrażenia wyznaczyć pracę wyjścia elektronu należy znać dwie wartości natężenia prądu nasycenia
oraz
przy tym samym napięciu anodowym oraz temperaturach żarzenia katody równych
i
. W związku z tym należy sporządzić dwie charakterystyki prądowo-napięciowe lampy przy danych temperaturach żarzenia katody.

Każdej temperaturze katody odpowiada inne natężenie prądu nasycenia. Im wyższa jest temperatura katody, tym większe jest natężenie prądu nasycenia. Z uzyskanych charakterystyk wyznacza się wartość prądu nasycenia odpowiadające różnym temperaturą katody, ale tej samej wartości napięcia anodowego. Temperaturę żarzenia katody można znaleźć wykorzystując zależność oporu katody od temperatury:

gdzie

opór w temperaturze T

- opór w temperaturze

temperaturowy współczynnik oporu (dla wolframu

)

skąd

przy czym
.

Opór
z dostateczną dokładnością można wyznaczyć z prawa Ohma:

gdzie
prąd żarzenia

napięcie żarzenia

Tabela pomiarów:

NUMER POMIARU	Iz=2,91 Uz=1,75		Iz=2,84 Uz=1,7		Iz=2,77 Uz=1,6		Iz=2,7 Uz=1,5
1	5	0,4	5	0,35	5	0,325	5	0,29
2	10	0,95	10	0,94	10	0,875	10	0,76
3	15	1,65	15	1,575	15	1,4	15	1,14
4	20	2,42	20	2,175	20	1,85	20	1,24
5	25	3,2	25	2,8	25	2,1	25	1,26
6	30	3,975	30	3,3	30	2,15	30	1,28
7	35	4,7	35	3,55	35	2,2	35	1,29
8	40	5,35	40	3,625	40	2,2	40	1,3
9	45	5,75	45	3,65	45	2,225	45	1,31
10	50	5,9	50	3,7	50	2,25	50	1,315

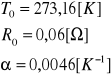
Wyniki pomiarów:

NUMER POMIARU	In [mA]	RT [Ω]	T [K]	Δ(RT) [Ω]	Δ(T) [K]
1	5,9	0,601	2234,66	0,017	59,89
2	3,7	0,599	2224,58	0,017	61,36
3	2,25	0,578	2148,59	0,017	62,88
4	1,315	0,556	2068,65	0,018	64,48

POMIAR	A [eV]	Δ(A) [eV]
	19,443	0,896
	4,257	0,149
	3,232	0,122
	2,319	0,183
	2,262	0,133
	2,211	0,274
	5,621	0,293

Obliczenia:

Jako prądy nasycenia przyjmujemy ostatni pomiar prądu anodowego, czyli:

In₁=5,9 mA In₂=3,7 mA

In₃=2,25 mA In₄=1,315 mA

Rezystancję temperaturową i maksymalny błąd bezwzględny pomiaru rezystancji obliczyliśmy na podstawie wzorów:

gdzie:

otrzymaliśmy więc:

R_T1=(0,601 ± 0,017) Ω R_T2=(0,599 ± 0,017) Ω

R_T3=(0,578 ± 0,017) Ω R_T4=(0,556 ± 0,018) Ω

Wartość temperatury i jej maksymalny błąd bezwzględny wyznaczyliśmy ze wzorów:

otrzymaliśmy więc:

T₁=(2234,66 ± 59,89) K T₂=(2224,58 ± 61,36) K

T₃=(2148,59 ± 62,88) K T₄=(2068,65 ± 64,48) K

Obliczeń pracy wyjścia i jej maksymalnego błędu wyznaczamy ze wzoru:

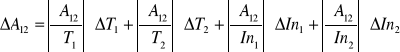
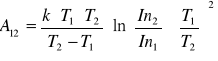
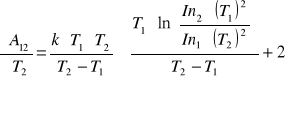
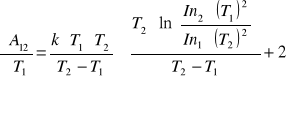
otrzymaliśmy:

A₁₂=( 19,443 ± 0,896) eV A₁₃=(4,257 ± 0,149) eV

A₁₄=(3,232 ± 0,122) eV A₂₄=(2,319 ± 0,183) eV

A₃₄=(2,262 ± 0,133) eV A₂₃=(2,211 ± 0,274) eV

Ostatecznie jako pracę wyjścia przyjmuje się średnią arytmetyczną uzyskanych wyników dla różnych par pomiarów:

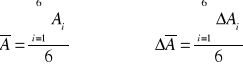
Ostatecznie więc otrzymujemy, że praca wyjścia termoelektronów w diodzie lampowej z katodą wolframową wynosi:

A=(5,623 ±0,293) eV

---
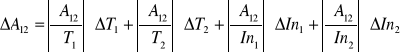
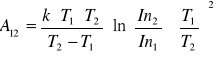
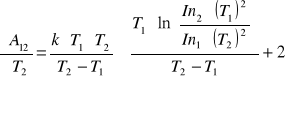
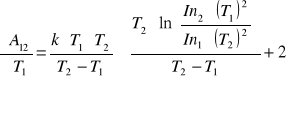