65611

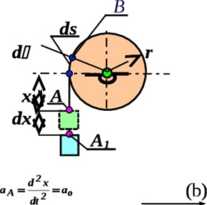
który może obracać się wokół poziomej osi, został przywiązany ciężar (rys.40). Ciężar ten zaczął opadać pionowo w dół ze stałym przyśpieszeniem liniowym o wartości a₀. Należy wyznaczyć prędkość kątową i przyśpieszenie kątowe bębna w dowolnej chwili oraz prędkość i przyśpieszenie liniowe punktu leżącego na obwodzie bębna. Promień zewnętrzny bębna równy jest r.

Rozwiązanie

Rys.40

Przyśpieszenie punktu A całkując (b) stronami otrzymamy:

y_A=°ot-ds dtp L

Vr = —= -r-r = «

=Ja_adt

dx

dLŻ^a°‘

(c)

Prędkość punktu B ^vr

dt dt

(d)

Prędkość punktu A jest identyczna jak punktu B, z (c) i (d)

a_n    da a„

mamy a> = -^t    e=—=~s-

Korzystając ze wzorów (57) mamy:

n —

Przykład 12    33kin

Przyśpieszenie kątowe e ciała poruszającego się ruchem obrotowym wyrażone jest w zależności od czasu t jako e=ą,e^_ar przy czym & i a oznaczają stałe. W chwili t = 0 prędkość kątowa ciała była równa zeru. Należy wyznaczyć prędkość kątową ciała (O jako funkcję czasu t.