68391

CYKL CARNOTA.
Rozważania dotyczą maszyny wyidealizowanej, w której procesy są odwracalne. Maszyna ta
wykonuje zamknięty cykl, po pewnej liczbie przemian wraca do stanu początkowego. Ciałem, które podlega pr., cyklicz jest gaz doskonały. Składa się z czterech cykli: 1) Rozprężanie izotermiczne w temp., Tj, 2) Rozprężanie adiabatyczne przy zmianie od Ti do T2, 3) Sprężanie izotermiczne w temp. Ta 4) sprężanie adiabatyczne od T2 do T|.
Pi(ViTi), W2T2), P3(V3T4), P4(V4T3)
|
Proc Ro 0 znr |
Ro zp |
Sp w |
Sp rę ża ad ia ba |
|
es ^ ęża nie izo ter |
ad ia ba t |
Izo ter | |
|
Z mi V, |
v2 |
v3 |
V4 |
|
ana —> |
—» |
-» |
-» |
|
objętv2 ości |
v3 |
v4 |
V, |
|
Zmia Ti |
T, |
”11 |
t2 |
|
na -eon |
=> |
eon |
-> |
|
temst. |
t2 |
st |
T, |
|
Praca W( |
W2 |
W3 |
W4 |
|
wyk=RT |
=Co |
=-R |
=c |
|
0 i* |
* |
T |
* |
|
nana ln |
(T2 |
*ln |
(T |
|
V,/V |
-T, |
.-t2 | |
|
) |
V, | ||
|
Ciepł Qi | |||
|
0 pobr ane |
0 |
Q2 |
) |

v3,|-*r2 =v2,,-,rIr2v4,,-, =vI,|-łrI
Proces adiabatyczny (Il i IV) możemy zapisać:
Otrzymujemy: (V3/V4)h,|=(WVi)h'1 czyli V:j/V4 = VyV,
Praca wykonana przy procesie izotermicznym III W3=RT2ln(WV4) W3=-RTJn(V,A/2) czyli W,=-W3 Suma prac w procesach adiabatycznych jest równa zeru
I
W=W|+W3 =R(Ti-T2)ln(Vj/V2). Z pierwszej zasady termo., dla przemiany izotermicznej gazu doskonałego mamy W=-Q ,Wi=RT iln(V i/V2)=-Qi
I analogicznie W3=-RTiln(Vi/V2)=QrQ2 W=W,+W3=R(T,-T2)ln(Vi/V2)=-(Qi+Q2)
ł
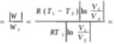
Wyszukiwarka
Podobne podstrony:
sumując, rozważania dotyczące procesu wartościowania cy można przyjąć:
12. MASZYNA BEZSZCZOTKOWA PRĄDU STAŁEGO Rozważymy obecnie maszynę, w której zasilanie jest odpowiedz
FIZA 3 / ****** w -- ->cpłnviti. pracujacsm według cykl* Carnota Cl
Image057 W dotychczasowych rozważaniach, dotyczących sposobów zapisu funkcji, funkcje te przyjmowały
skanuj0161 (2) 169 Powyższe rozważania dotyczyły kształtowania się produkcyjności całkowitej, kratko
Wstęp Rozważania dotyczące genezy, rozwoju i recepcji filozofii takich myślicieli, jak Immanuel Kant
skrypt wzory i prawa z objasnieniami64 126 Cykl Carnota. Druga zasada termodynamiki Termodynamika 12
IMG?54 Opisane powy żej zawiadomienia dotyczą działania prokuratorów ty procesowe w postępowaniu V D
16983 Slajd70 (16) Uwaga druga, a zarazem swoista konkluzja tych rozważań, dotyczy użyteczności
65 Problem własności w dokumentach papieskich - analiza ekonomiczna Podsumowując rozważania dotycząc
instr 9 9 str.Hł Rozważania dotyczące Zadania Nr.5 Na czym polega różnica pomiędzy liniowym i propor
P1090818 płeć /osi zmienną zdecydownnio różnicującą upodobania. k t*Jnioz* w dalszych rozważaniach d
Odlewanie pod dśnieniein Pizeprowadza się go zawsze w maszynie odlewniczej, w której zamocowane są c
Podstawowe rozważania dotyczące najpopularniejszego pieca indukcyjnego tyglowego. Oprócz podstawowyc
17 Wojciech DziedziakO POJMOWANIU PRAWA - ZARYS PROBLEMU Celem niniejszych rozważań dotyczących
więcej podobnych podstron