82379

Część 1

14. RAMY PRZESTRZENNE STATYCZNIE NI EW YZNACZ ALNE

4

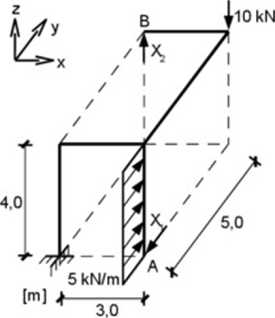
Rys. 14.2. Układ podstawowy z me wiadomymi silami X i X:

który nnisi spełniać warunki kinematycznej zgodności z układem wyjściowym. Oznacza to. że przemieszczenie punktu^ po kierunku osi y oraz przemieszczenie punktu B po kierunku osi _ muszą być równe zero.

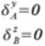
Na powyższe przemieszczenia wpływ mają nadliczbowe siły X, oraz obciążenie zewnętrzne. Równania kanoniczne pizyjmą zatem postać:

(14.7)

6’-6„X_l+6_oX_i+6„-0 6\=6_U X, +S_2! X_: +6_:f=0

Przemieszczenia w ramie przestrzeiuiej obliczymy pomijając wpływ sil normalnych i tnących:

M,M_dt j V f M\M\

EJ.

!■

GJ.

-ds

(14.8)

gdzie:

M'. \1\. M]. A/; - momenty zginające działające odpowiednio względem osi v i z.

M] , M\    - momenty skręcające względem osi pręta,

J,    - moment bezwładności na skręcanie.

Ponieważ pizekrój pręta jest kołowy, to J_} = J_: =J . a moment na skręcanie jest równy biegunowemu momentowi bezwładności J, = J₀ = J_: + /,. = 2J. Podstawiając dane GiJ, otrzymamy:

i* M, A/1    rn (■ iW. iW i    ^—• r

EJ

EJ

M,M'_k 0,75 EJ

ds

(14.9)

Kolejnym etapem jest wyznaczenie wartości momentów zginających i skręcających od sił jednostkowych przyłożonych kolejno w miejsca niewiadomych^/ i X;, oraz od obciążenia zewnętrznego.

AlmaMater

Dobra D., Jambrożek S.. Komosa M., Mikołajczak E.. Przybylska P.. Sysak A.. Wdowska A.