82377

Część 1

14. RAMY PRZESTRZENNE STATYCZNIE NIEWYZNACZALNE

1

14.

14. RAMY PRZESTRZENNE STATYCZNIE NIEWYZNACZALNE

14.1. Wstęp

Układ przestrzelmy - to konstrukcja, której elementy ułożone są w trzech wymiarach (r. y. z). Układem przestrzennym jest także konstrukcja płaska wpisana w płaszczyznę, na którą działają siły prostopadłe do tej płaszczyzny (kierunek ich działania pokrywa się z trzecim wymiarem).

/I----’A

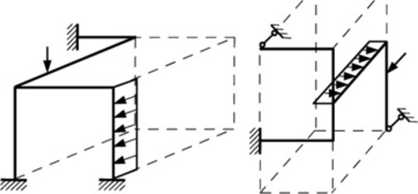
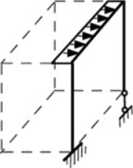
Ramy przestrzenne statycznie niewyznaczalne rozwiązujemy analogicznie jak układy płaskie.

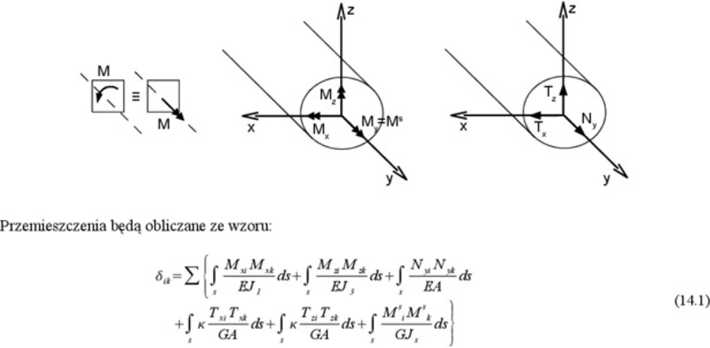
W celu obliczenia przemieszczeń należy określić siły, jakie występują w pizekiojach ustroju piętowego. W układach pizestizennych rozróżniamy siły działające wzdłuż trzech osi, momenty zginające w dwóch płaszczyznach i moment skręcający. Moment działający wokół osi zaznaczamy jako wektor z podwójnym grotem wzdłuż tej osi (przyjmujemy oznaczenia jak dla układów prawoskrętnych).

AlmaMater

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.