82403

Część 2 14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY 16

P(x.t)

X

P(x.t)

u(x.t)

N(x.t)|—1 r(x,t)

I_I N(x.t)4

3N(x,t)

dx

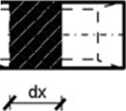
Rvs. 14.11. Element dx belki

Wszystkie wartości sil p. N, r, są funkcjami położenia i czasu f\x,t). Opór ruchu, czyli siła bezwładności wynosi:

,    d²u(x,t)

r\x,t\ = -dm-_;—

dr

Masę wycinka wyznaczamy mnożąc jego objętość przez gęstość:

dni=Apdx

Zapisując równanie równowagi ]T X=0 otrzymujemy:

/)+#(*,/)+' ^ ,^X    (h + p{.\, t)dx-Apd\^{( u}'\^r=0

dx    er

Dla przypadku drgań swobodnych ( p\ x, t)=0) mamy:

<5AfU,/) ,    , <?u(x,t)

——dx-Apdx-

dt²

Wiedząc, źe stan naprężeń wywołany działaniem siły podłużnej określa związek fizyczny:

N=a.A=t.EA=^^-EA

(14.9)

dx

(14.10)

zapisujemy równanie falowe:

^;<fu{x,t\ c^:u[x,t) _Q dx^:    dt²

(14.11)

gdzie:

E EA P P

(1412)

Podobnie jak w przypadku drgań poprzeczny cli wprowadzamy do zapisu rozdział zmiennych. Przemieszczenie jest iloczynem funkcji U zależnej tylko od przestrzeni i funkcji T zależnej tylko od czasu:

Dobra D.. Dztakicwlcz L, Jambrożrk S.. Kotnona M.. Mikołajczak K., Przybylaka P., Sytak A.. Wdowdca A

AlmaMater