85192
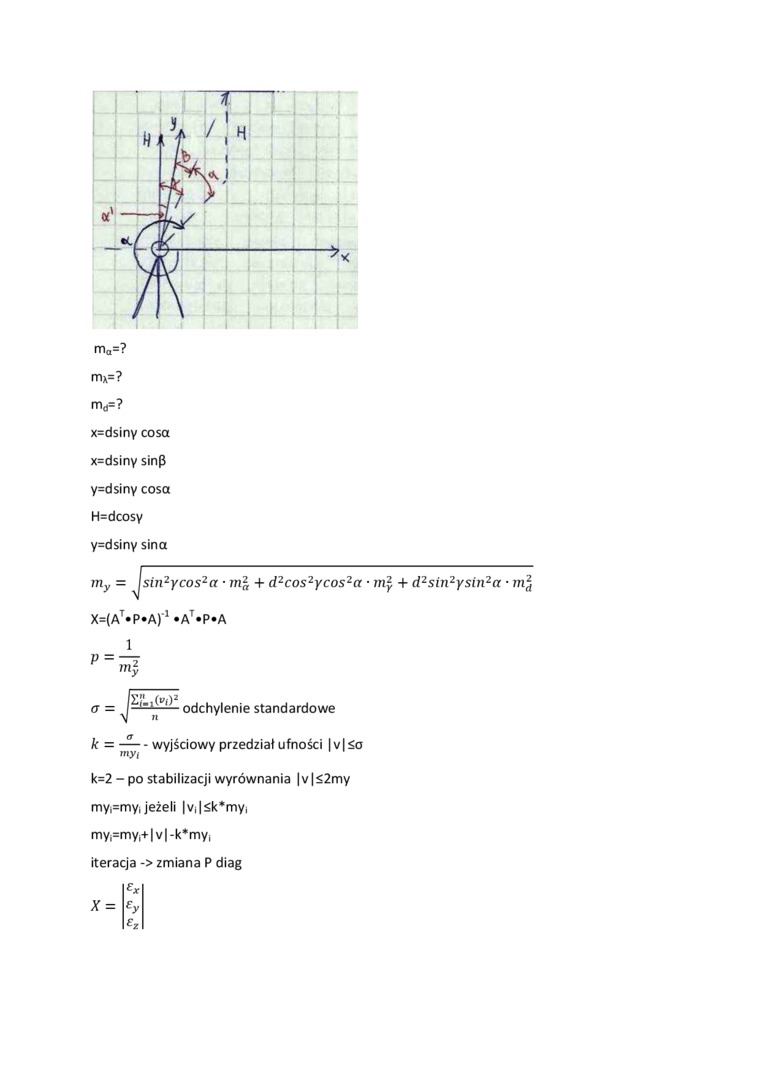
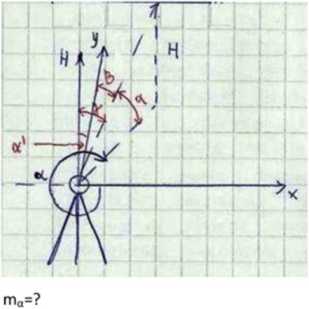
mx=?
md=?
x=dsiny cosa x=dsiny sin(3 y=dsiny cosa H=dcosy y=dsiny sina
sin2ycos2a • m2 + d2cos2ycos2a • m2 + d2sin2ysin2a •
X=(At*P»A)'1 »At»P»A
J2-' (w)2
— odchylenie standardowe -2—- wyjściowy przedział ufności |v|<o
k=2 - po stabilizacji wyrównania |v|<2my my,=myi jeżeli |Vj|£k*myj myj=myi+| v|-k*myj iteracja -> zmiana P diag
Wyszukiwarka
Podobne podstrony:
HPIM0550 /O tMML . ma-f -siki md demo. cim ~So Sin izrt ufl. feoo ujToruu mttruxi_ Sf« uEel
Kolendowicz&5 Th = K^cosa — //Msina — wh sina — qx cosa dla 0 ^ x ^ — dla x = 0 Tu
img119 cos x -f i sin o- f COS ar = ±(eł* + e-«) [sina- = - e~ix)
Wzory redukcyjne II WZORY REDUKCYJNE II sin(90°-a) = cosa sin(90°+a) = cosa cos(90°-a)=
DSC00064 (2) m a, którego sin« = —
(3) (3) G, G, sina
MAT18 18 2(1 l / -> 1 7 _et_= r_z±T_= r +1 )dt = sin.v(
Twierdzenie Sinusów: sina sini _ sine sin .,4 sin B sinCTwierdzenie cosinusów dla boków: cosa= cosic
1 0 0 1 0 0 1 0 0 Rotx(a) ~ 0 cosa —sina = 90° -> 0 0 -1 ;-90°
mech2 125 248 stąd N - G cosa - P sin {3 = 0. Rys. 177 Warunek ruchu bez poślizgu jest następujący:
mech2 125 248 stąd N - G cosa - P sin {3 = 0. Rys. 177 Warunek ruchu bez poślizgu jest następujący:
mech2 70 *Y t*= -2,42 m X = X, X = -G ain a - P + P X = -mg sina - f mg cosa+ P, ~ m x = -mg sin a-
więcej podobnych podstron