mech2 70

*Y

t*= -2,42

m X = X,

X = -G ain a - P + P

X = -mg sina - f mg cosa+ P,

~ m x = -mg sin a- f mg cos a + P,

138,

skąd 5,86 + 49,1 = -2,42 + 7,41 s.

Ostateoznie

t = 4,99 B.

Prędkość jest równa zeru, gdy x* = 4,99 s, ale (t^ - tg) < t * , dlatego nie nastąpi zmiana prędkości w rozpatrywanym przedziale ozasu (t^ - t^).

4. Sprawdzimy otrzymaną w chwili t^ wartość prędkości , stosują., równanie dynamiczne ruchu: przy czym lub

stąd

to jest    ..    p

x = -g ain a - fg cosa + — ,

przy czym P = t - równanie prostej OB, i dlatego x = -g(sina + f oosoO + ^ t. Całkując to równanie różniczkowe, otrzymujemy

x = -g(sin a+ f coso^t + rj t + C.

Do określenia stałej całkowania C wykorzystamy warunek początkowy zadania: dla t = 0 v_Qx = x_Q = 10 ra/s. Otrzymujemy stąd C = 10 id/b. Zatem równanie określająoe zmianę prędkości w przedziale czasu od 0 4° ^ przyjmie postać

x= -g(sin a+ f oosoOt + t^ + 10.

Gdy t = 3 s

v₁ = ^ = -9,81(0,5 + 0,1-0,87) * 3 + H • 9 + 10 = 2,10 m/s.

1.6. Zastosowanie zasad dynamiki do badania ruchu punktu materialnego nie swobodnego

Zadanie D-6

Eulka, przyjęta za punkt materialny, porusza się z położenia A wewnątrz rurki w płaszozyźnie pionowej (rys. 81-83). Znaleźć prędkość lulki w'położeniach B i C i ciśnienia kulki na ściankę rurki w położeniu C. Tarcie na krzywoliniowych odoinkach trajektorii pominąć. W wariantach: 3,6,7,10,13,15,17,19,25,28,29 kulka przebywa drogę h₀ oddzielając się od sprężyny.

Dane do rozwiązania poszczególnych zadań zestawiono w tabeli 26.

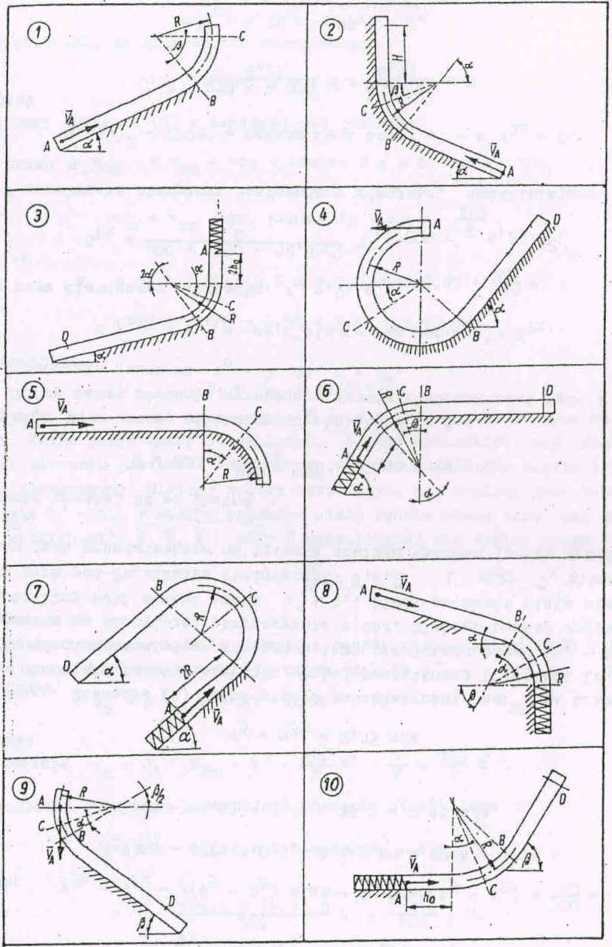
i

Rys. »1