87955

Dynamiczne równania mchy punktu materialnego.

Dynamiczne równania mchy w postaci wektorowej F_x =m x_t F_y =my, F_t = ni z

Równania ruchu w naturalnym układnie współrzędnych dv    v²

dr    r    ^{b b}

Zasada pędu masy i impulsu siły dla układu punktu materialnego.

Pęd punktu materialnego jest wektorem stałym jeżeli suma geometryczna sil działających na punkt jest równa zeru.

Fdt =d(mv) gdzie _

Impuls elementarny siły działającej na punkt materialny jest równy przyrostowi elementarnemu pędu tego punktu.

12 -

Fdt = d fi

ll

Kręt układu punktu materialnego.

Krętem poruszającego się punktu materialnego względem obranego bieguna 0 nazywamy wektor równy iloczynowi wektorowemu promienia r przez pęd p poruszającego się punktu. Kręt jest więc momentem pędu (momentem ilości mchu) względem obranego bieguna.

K° = mom_t,p = r* mv

Pochodna wektora krętu względem czasu jest równa mometowi głównemu wszystkich sił działających na dany punkt materialny.

ruch układu o zmiennej masie

Jako podstawę przyjmujemy tu 2 zasadę dynamiki /Newtona dla układu materialnego- zasadę pędu

d(mv_s)

dt

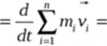
F

Zakładając, że od układu odrywa się z Prędkością Vb masa dm określimy elementarną

zmianę wektora pędu układu

d(mv_s) =mv_s —[(m —dm)(v_s —dv_s) +dmv_h ]

Przy czym mvs- wektor pedli układu przed oderwaniem się masy dm, (m —dm)(v₁ —dv_s) -+-dmv_b -ped układy po oderwaniu się masy dm.

Definicja i równanie pracy siły stałej