88899

Macierz transformacji C, występująca w powyższych wzorach nazywana jest też często macierzą obrotu lub macierzą kosinusów kierunkowych. Jest to macierz ortonormalna, charakteryzująca się tym, że jej wyznacznik jest równy 1, a macierz odwrotna jest równa macierzy transponowanej:

Opisana powyżej transformacja dotyczy pojedynczego węzła, jednak przejście do całego elementu wymaga na ogól tylko „powielenia” omawianej tu macierzy na diagonali pełnej macierzy transformacji dla elementu. W elemencie ramy płaskiej macierz ta ma postać:

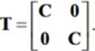
W ogólnym przypadku możliwe jest zastosowanie tzw. układów węzłowych, wtedy macierz górna i dolna w powyższym wzorze mogą się różnić, ale ogólna zasada pozostaje bez zmian. Istotne jest, że macierz T jest również ortonormalna. Ostatecznie więc lokalne wektory przemieszczeń i sił węzłowych w elemencie można sprowadzić do odpowiadających im wektorów w układzie globalnym:

q = TQ p = TP

Po podstawieniu tych zależności do równań równowagi elementu: kq = p => kTQ = T P

i lewostronnym wymnożeniu przez T^t otrzymamy równania wyrażone w układzie globalnym, T^xkTQ = T^TTP, ale T^XT = I, więc T^TkTQ = P skąd ostatecznie wynika, że macierz elementu w układzie globalnym można zapisać jako:

K = T^TkT.

Podsumowując, przed złożeniem (agregacją) globalnej macierzy sztywności wszystkie lokalne macierze elementów transformowane są wg powyższego wzoru do wspólnego globalnego układu współrzędnych.

Elementy izoparametryczne

Elementy skończone mogą mieć bardziej skomplikowany kształt niż przedstawiono to na ostatnim wykładzie, co ma duże znaczenie dla efektywnego generowania siatek MES w obszarach nieregularnych lub w zagęszczaniu tych siatek w wybranych strefach kontinuum.

W niniejszym punkcie przedstawiamy ideę zastosowania tzw. izoparametrycznych elementów skończonych i sposób obliczania macierzy sztywności elementu przy zastosowaniu całkowania numerycznego (na podobnych zasadach obliczany jest również wektor prawych stron od obciążeń elementowych). Opisany poniżej sposób przejścia od elementów regularnych do elementów dowolnego kształtu jest również swego rodzaju transformacją, jednak jej istota jest zupełnie odmienna od tej prezentowanej w poprzednim punkcie.