89698

2. Całki podwójne. potrójne i krzywoliniowe Chemia, II semestr 2

3.    Zmienić kolejność całkowania w podanej calce, a następnie policzyć ją:

v/2

e 1    4 2z    3    x+3    2 arcawy

a) J dx J 2xe^ydy b) j dx J A^dy c) J dx J xdy d) J dy J dx

1 lnx    1 x    -2 x^a-3    0 areśnj/

4.    Wprowadzając współrzędne biegunowe, policzyć całki:

a)    JJ ^1U^ J 2 ^ dxdy D = {(x.y) : 1 < x² + y² < 4, y > 0}:

D

^b)    JJ ₍₁    D = {(x.y) :x² + y²<y, y> x};

D

c)    JJ {x²+y²)dxdy D = {(x, y) : y < x² + y² < x, y > 0}.

D

5.    Policzyć |X)le obszaru D :

a)    D = {(x, y):x + y< 3, y² < 4x y> 0}:

b)    D    obszar ograniczony prostymi: x - 2y = 0, x — 2y = 3,    y = 2x — 9, y = 2x — 6;

c)    D    obszar ograniczony krzywymi: y = e^x, y = In ar, x + y    = 1, x = 2;

d)    D    obszar ograniczony krzywymi: x² + y² = 1, x² + y² =    4, x = v/3y,    y =    \/3x:

e)    D    = {(x,j/) : x² + y² < 2x, y > x};

f)    D    = {(ar, j/) : x² + y² < 2y, y> \/3|x|};

g)    D jest ]X)łożoną w I ćwiartce częścią koła: (x — l)² + (y — l)² < 2.

6.    Korzystając z całki podwójnej obliczyć objętość:

a)    bryły ograniczonej ix)\vierzcliniami: x² 4- y² = 1, x + y + z — 3, 2 = 0:

b)    ostrosłupa, ograniczonego płaszczyzną x + y + z = 1 i płaszczyznami układu współrzędnych;

c)    słupa między powierzchnią walca o promieniu a. którego osią jest Oy. a trójkątem O AD. gdzie 0(0.0.0), j4(a,0.0), D(a.a.O):

d)    bryły ograniczonej ix)wierzcliniami: x² + y² = 2y, z = x² + y². z = 0.

Całki potrójne

Obszar V położony w przestrzeni /?^:ł nazywamy normalnym względem płaszczyzny Oxy, jeśli istnieją dwie funkcje ciągłe , il> na obszarze D (będącym rzutem V na płaszczyznę Oxy takie, że V = {(x, y. z) : {x,y) € D,tp(x,y) < z < ip(x.y)}. Wtedy całka potrójna z funkcji ciągłej / po obszarze V wyraża się następującym wzorem:

JJJ f(x,y, z) didydz

V

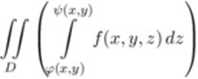
VKx,v)

dx dy = JJ dx dy I f(x,y,z)dz

D    vKx.y)

•    Współrzędne walcowe: przyjmujemy x = rcosp.y = rsin^, z = z. Wtedy ./ = r.

•    Współrzędne sferyczne: x = rcos^cosd.y — rsin<£costf, 2 = rsind. Wtedy J — r²costt