89971

Wykłady z Procesów Dyfuzyjnych - Projektowanie kolumn ekstrakcjnych Wojciech Skrzypriiski

u_R=u_kexp(-x)    (2)

u_R = u_k exp(- b x)    (3)

^uR = ii_k(l-x)exp(-b_Ix)    (4)

u_R=u_k a-xr    (5)

u_R = u_k (l - b₂ x)    (6)

u_R = u_k(l-x)^n,(l+b₃x)    (7)

u_R =u_k (l-x)T^ł + b₄ x    (8)

oraz —+ -^^£- = u_k (l-x)    (9)

x l-x

Równania tc mogą służyć do wyznaczenia granicznych prędkości obu faz, przy których występuje zalewanie kolumny W tym celu należy obliczyć pochodne i przyrównać je do zera:

dud	= 0
dx		dx

Dla znanej wartości stosunku strumieni faz, czyli dla znanego stosunku prędkości obu faz:

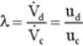
można obliczyć prędkości faz w punkcie zalewania zrównali:

Równanie	Umowne prędkości faz |m7(m’s)|	Stosunek strumieni
1	tldf = 2uk x^2(l-xf) =uk (l-xfJ^2(l-2xf)	X.rjsi-Vifi=s] l-2xf
2	^uar^= uk ^Xr (2-xf )exp(-xf) urf =uk (l xf )* exp(- xf)	U-hJizlL V, 1 — xf J 1-Xf
3	^udf = ^uk ^xr [l + b (1 - Xf )]exp(- b xf) Urf =uk (l-Xf)^2(l-bxf)exp(-bxf)	X =	^Xf [l-Xf	1+ b(l-xf) l-bxf
4	udr = uk xf^2 (1 -xf )[2 + b, (1 -xf )]exp(- b, x,) Urf = Ukd-Xf)^2 {l-xf[2+b, (1 - xf ®exp(- b, xf)	x-f ^Xf [1-Xf	V, , 2 + b, (l - xf) ^f 1 - xf [2 + b, (1 - xf)]
5	u* =ukxf^2(in + l)(l-xj^nucf = uk (1 - xf f (1 - xf j^ml)[l - xf (m +1)]	X =	\ ^xf	' (m+ l)(l-xf) l-(m+l)xf
6	^udf =Uk xj[l + b2 (l — 2 xf)] urf =uk(l-xf)^2(l —2b2 xf)		,\J	1+ b; (1- 2 xf) l-2b, xf
7	udf = uk xf^2 (1 - xf r [l+m, (1 + b3 xf)+ b,] u«f^=uk (i^_ Xf) (i-Xfr jl + ,_^fx I^ml(^1+bJ^xf)^+2b»]J	>-fe)	l + m, (l + b, xf)+b, 1 + p^-K (l+b,xf + 2b,)] 1-Xf

2