91101

G(s) liniowym układu (Obiektu) liniowego stacjonarnego nazywać będziemy wartość określoną jako stosunek transformaty wymuszenia U(s) tego układu przy zerowych warunkach początkowych. G(s) =Y(s) / U(s)

TYPOWE CZŁONY LINIOWE

-    Człon proporcjonalny

-    Człon inercyjny I rzędu

-    Człon całkujący idealny( na YVY jest całka)

-    Człon całkujący z inercją! to samo, tylko zaburzone)

-    Człon różniczkujący( na WY pochodna sygnału WE)

-    Człon różniczkujący z inercją! to samo ale zaburzony)

-    Człon oscylacyjny( złożenie członów inercyjnych inercyjnych rzędu)

-    Człon oscylacyjny II rzędu

-    Człon opóźniający( to co na WE opóźnione na WY)

CZŁON BEZINERCYJNY ( proporcjonalny wzmacniający)

Równanie różniczkowe WE/W Y:    y= ku

k - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia w stanie ustalonym.

T - stała czasowa = 0

Charakterystyka skokowa:    g(t)

t

h(t) = kl(t)

Charakterystyka impulsowa:    h(t)

h(t) = k ó(t)

Transmitacja:

Gi(s) = k

Kierunek przepływu pi^tn

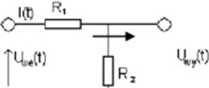
** Przykład 1: CZWÓRNIK (Dzielnik Napięcia)

Wybieram wielkości WE i WY czwómika, zakładam jeszcze, że jest nieobciążony.

o

O

I(t) - prąd płynie, wiedzieć to musze, aby znać zależności między U_w«(t) i Uwy(t).

iMt) = i(t) - (R, -ma—

lUt) = 1(0 * r₂ => I(t) wyliczam l(t) i podstawiam

R

+ R a