91941

Układ opisany równaniami stanu i równaniami wyjścia może być przedstawiony w formie schematu blokowego.

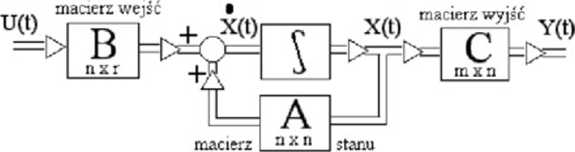
Rys Schemat blokowy układu opisanego równaniem stanu i równaniem wyjścia

Przedstawiony model układu dynamicznego można traktować jako podstawowy schemat opisany równaniami stanu i równaniami wyjścia.

Schemat ten ulega modyfikacjom zależnie od równań stanu i równań wyjścia.

Równania stanu i równania wyjścia zależą od własności danego układa

A. Przypadek jednowymiarowego układu sterowania, gdy wektory U(t) i Y(t) są reprezentowane przez odpowiednio przez pojedyncze składowe u(t) i y(t).

o dla U(t)=u(t) macierz B staje się macierzą kolumnową b o wymiarach nxl,

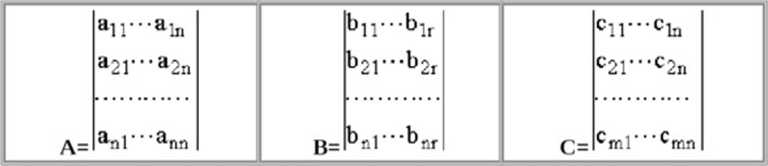
		Macierze b i c:
	bil		Równania stanu:
	^b21		X(t) = A ■ X(t) + b • u(t)
b=	bnl	C=|^c11» ^c12»'"»^cln|	>< u II ;>»

o^da^ęO^^O^^derz^C^steje^inwdera^^erezo^c^ow^raaracłi 1 x n.

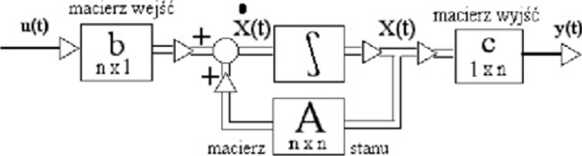
Rys Schemat blokowy układu gdy wektory TJ(t)=u(t) i Y(t)=y(t) są jednowymiarowe

C. Przypadek układu dynamicznego, gdy sygnały sterujące oddziaływują także na sygnały wyjściowe U(t)^-^Yft). W tym przypadku równanie wyjścia Y(t)=Y[X(t), U(t)l zostaje rozbudowane o macierz D.