94110

produktu po danej cenie. W tym miejscu korzystamy z przyjętego na początku rozważali o przedsiębiorstwach uproszczenia, że produkcja wytworzona jest równa produkcji sprzedanej. Tym samym w warunkach monopolu oferenta będziemy mogli korzystać z następującej właściwości: podaż monopolisty jest równa popytowi na jego produkt, czyli:

y=x

Znając funkcję popytu monopolista może określić wielkość przychodu jaki osiągnie dla różnych kombinacji wielkości produkcji i ceny. W dalszej analizie ograniczymy się do rozpatrzenia tylko najprostszego przypadku tzn. gdy funkcja popytu a tym samym i funkcja cena-zbyt jest prostą o ujemnym nachyleniu. Wzór ogólny na taką prostą będzie w naszym przypadku następujący:

p = a - by

gdzie: a. b parametry funkcji większe od zera

Aby lepiej uzmysłowić sens ekonomiczny tych parametrów rozpatrzmy prosty przykład. Powiedzmy, że Miejskie Przedsiębiorstwo Komunikacyjne w danej miejscowości ustaliło w oparciu o odpowiednie badania rynku, że gdyby cena biletu wynosiła 10 zł, to przewozy spadłyby do zera. gdyż np. przejazd taksówką w granicach miasta obsługiwanego przez to MPK byłby tańszy. Z kolei wiadomo, że gdyby przejazdu środkami publicznej komunikacji były darmowe, to dziennie korzystałoby z nich maksymalnie 100 tys. osób. Jeżeli ilość pasażerów malałaby proporcjonalnie wraz ze wzrostem ceny biletu, to finikcja popytu na przejazdy byłaby prostą o następującym wzorze: p= 10 - O.OOOly. Parametr a jest równy 10. natomiast b = 0,0001. Pierwszy z nich pokazuje tzw. cenę zaporową, czyli taką cenę przy której popyt spada do zera. Wynosi ona 10 zł. Natomiast drugi parametr b określa tempo w jakim będzie musiała maleć cena aby przewozy wzrosły o jednego pasażera, czyli obniżka ceny o 1 gr (0.01 zł) spowoduje wzrost przewozów o 100 osób. Wróćmy ponownie do wzorów ogólnych.

W naszym przypadku finikcja przychodu monopobsty będzie wyglądała następująco:

E = py = y(a - by) = ay • by²

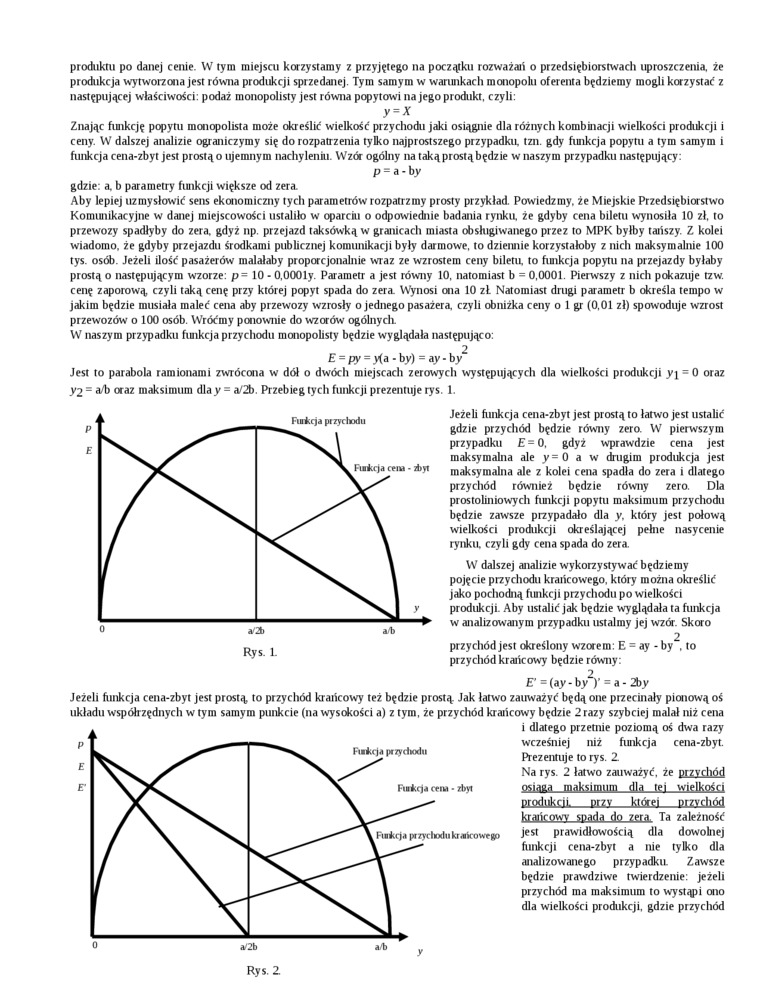
Jest to parabola ramionami zwrócona w dół o dwóch miejscach zerowych występujących dla wielkości produkcji y\ = 0 oraz y2 = a/b oraz maksimum dlay = a 2b. Przebieg tych funkcji prezentuje rys. 1.

Jeżeli funkcja cena-zbyt jest prostą to łatwo jest ustalić gdzie przychód będzie równy zero. W pierwszym przypadku £ = 0. gdyż wprawdzie cena jest maksymalna ale y=0 a w drugim produkcja jest maksymalna ale z kolei cena spadła do zera i dlatego przychód również będzie równy zero. Dla prostoliniowych funkcji popytu maksimum przychodu będzie zawsze przypadało dla y. który jest połową wielkości produkcji określającej pełne nasycenie rynku, czyli gdy cena spada do zera.

W dalszej analizie wykorzystywać będziemy pojęcie przychodu krańcowego, który można określić jako pochodną funkcji przychodu po wielkości produkcji. Aby ustalić jak będzie wyglądała ta funkcja w analizowanym przypadku ustalmy jej wzór. Skoro

. 2 by .to

przychód jest określony wzorem: E = ay przychód kraiicowy będzie równy:

£' = (ay - by )’ = a - 2by

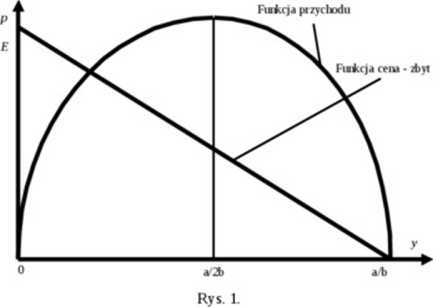
Jeżeli funkcja cena-zbyt jest prostą, to przychód krańcowy też będzie prostą. Jak łatwo zauważyć będą one ptzecinały pionową oś układu współrzędnych w tym samym punkcie (na wysokości a) z tym, że przychód krańcowy będzie 2 razy szybciej malał niż cena

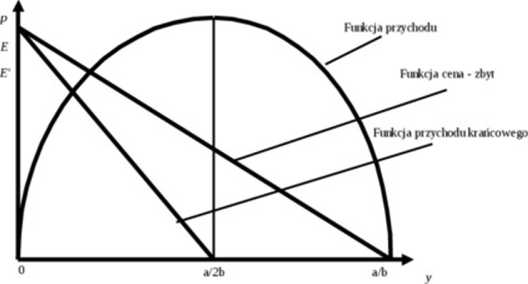
Rys. 2

i dlatego przetnie poziomą oś dwa razy wcześniej niż funkcja cena-zbyt. Prezentuje to rys. 2

Na rys. 2 łatwo zauważyć, że przychód osiaŁa maksimum dla te i wielkości prodnkcii- przy której przychód kraikowv spada do zera. Ta zależność jest prawidłowością dla dowolnej funkcji cena-zbyt a nie tylko dla analizowanego przypadku. Zawsze będzie prawdziwe twierdzenie: jeżeli przychód ma maksimum to wystąpi ono dla wielkości produkcji, gdzie przychód