94125

produkcji, gdyż krzywa K_Cp leży wtedy powyżej p, czyli wytworzenie jednostki produktu kosztuje więcej niż wynosi jego cena.

0 Ceng nazywa sig ceiiąpiogu zysku, Łdyż pizedsicbiorspyp w najlepszym pizypadku. pizy wybiauiii optymalnej wielkości produkcji może Mgdy osiągnąć zgrywy zysk Cena ta swoją wysokością odpowiadanajniższym przeciętnym

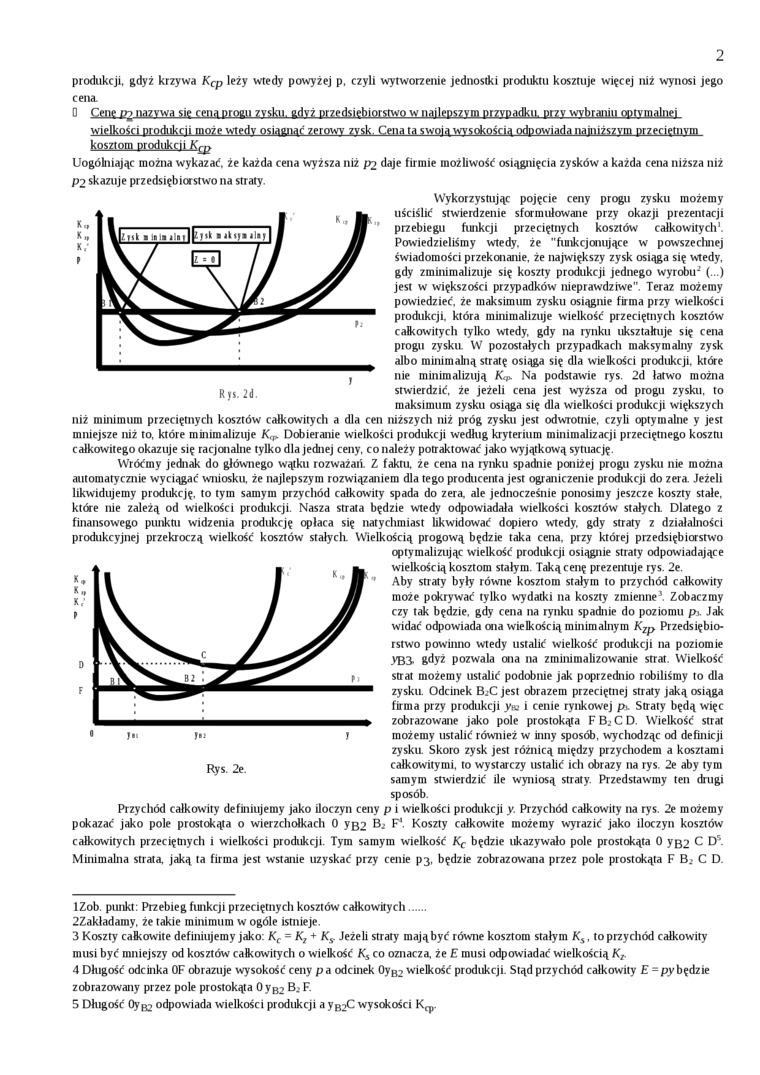
Uogólniając można wykazać, że każda cena wyższa niż p2 daje firmie możliwość osiągnięcia zysków a każda cena niższa niż P2 skazuje przedsiębiorstwo na straty.

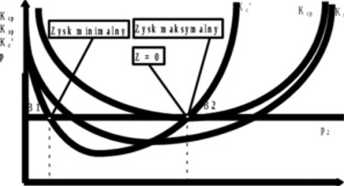
Rys. 2d

Wykorzystując pojęcie ceny progu zysku możemy uściślić stwierdzenie sformułowane przy okazji prezentacji przebiegu funkcji przeciętnych kosztów całkowitych^{1 2 3 4 5}. Powiedzieliśmy wtedy, że "funkcjonujące w powszechnej świadomości przekonanie, że największy zysk osiąga się wtedy, gdy zminimalizuje się koszty produkcji jednego wyrobu*’ (...) jest w większości przypadków nieprawdziwe". Teraz możemy powiedzieć, że maksimum zysku osiągnie firma przy wielkości produkcji, która minimalizuje wielkość przeciętnych kosztów całkowitych tylko wtedy, gdy na rynku ukształnije się cena progu zysku. W pozostałych przypadkach maksymalny zysk albo minimalną stratę osiąga się dla wielkości produkcji, które nie minimalizują Kup. Na podstawie rys. 2d łatwo można stwierdzić, że jeżeli cena jest wyższa od progu zysku, to maksimum zysku osiąga się dla wielkości produkcji większych niż minimum przeciętnych kosztów całkowitych a dla cen niższych niż próg zysku jest odwrotnie, czyli optymalne y jest mniejsze niż to, które minimalizuje K^ Dobieranie wielkości produkcji wedhig kryterium minimalizacji przeciętnego kosztu całkowitego okazuje się racjonalne tylko dla jednej ceny, co należy potraktować jako wyjątkową sytuację.

Wróćmy jednak do głównego wątku rozważali Z faktu, że cena na rynku spadnie poniżej progu zysku nie można automatycznie wyciągać wniosku, że najlepszym rozwiązaniem dla tego producenta jest ograniczenie produkcji do zera. Jeżeli likwidujemy produkcję, to tym samym przychód całkowity spada do zera, ale jednocześnie ponosimy jeszcze koszty stałe, które nie zależą od wielkości produkcji. Nasza strata będzie wtedy odpowiadała wielkości kosztów stałych. Dlatego z finansowego punktu widzenia produkcję opłaca się natychmiast likwidować dopiero wtedy, gdy straty z działalności produkcyjnej przekroczą wielkość kosztów stałych. Wielkością progową będzie taka cena. przy której przedsiębiorstwo

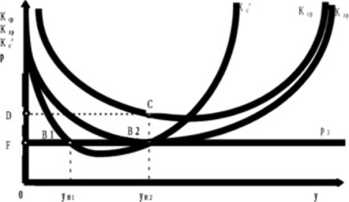
Rys. 2e.

optymalizując wielkość produkcji osiągnie straty odpowiadające wielkością kosztom stałym. Taką cenę prezentuje rys. 2e.

Aby straty były równe kosztom stałym to przychód całkowity może pokrywać tylko wydatki na koszty zmienne*. Zobaczmy czy lak będzie, gdy cena na rynku spadnie do poziomu p* Jak widać odpowiada ona wielkością minimalnym K₂p Przedsiębiorstwo powinno wtedy ustalić wielkość produkcji na poziomie yB3. gdyż pozwala ona na zminimalizowanie strat. Wielkość strat możemy ustalić podobnie jak poprzednio robiliśmy to dla zysku. Odcinek B*>C jest obrazem przeciętnej straty jaką osiąga firma przy produkcji yi« i cenie rynkowej p_t Straty będą więc zobrazowane jako pole prostokąta F Bj C D. Wielkość strat możemy ustalić również w inny sposób, wychodząc od definicji zysku. Skoro zysk jest różnicą między przychodem a kosztami całkowitymi, to wystarczy ustalić ich obrazy na rys. 2e aby tym samym stwierdzić ile wyniosą straty. Przedstawmy ten drugi sposób.

Przychód całkowity definiujemy jako iloczyn ceny p i wielkości produkcji y. Przychód całkowity na rys. 2e możemy pokazać jako pole prostokąta o wierzchołkach 0 yg2 F*. Koszty całkowite możemy wyrazić jako iloczyn kosztów całkowitych przeciętnych i wielkości produkcji. Tym samym wielkość K_c będzie ukazywało pole prostokąta 0 yg2 C D\ Minimalna strata, jaką ta firma jest wstanie uzyskać przy cenie P3, będzie zobrazowana przez pole prostokąta F B.» C D.

1

IZob. punkt: Przebieg funkcji przeciętnych kosztów całkowitych......

2

2Zakładamy. że takie minimum w ogóle istnieje.

3

   Koszty całkowite definiujemy jako: K_c = K_z+ K_s. Jeżeli straty mająbyć równe kosztom stałym K_s. to przychód całkowity musi być mniejszy od kosztów całkowitych o wielkość K_s co oznacza, że £ musi odpowiadać wielkością Kr

4

   Długość odcinka OF obrazuje wysokość ceny pa odcinek 0y_B2 wielkość produkcji. Stąd przychód całkowity £ = py będzie zobrazowany przez pole prostokąta 0y_B2 B.> F.

5

   Długość Oy^ odpowiada wielkości produkcji a y_B2C wysokości K<p.