96038

wyników pomiarowych. Te przybliżone wartości błędów noszą nazwę wskaźników dokładności pomiarów.

1. Błędy przypadkowe w pomiarach bezpośrednich

Probabilistyczna teoria błędów Gaussa

Z jednego pomiaru nie możemy wnioskować o jego dokładności. Do tego konieczna jest icli seria. Otrzymujemy ją przez kilkukrotne, niezależne powtórzenie rozpatrywanego pomiaru. Wyniki w

serii będą różnić się losowo. Oznaczmy je X1X2X1.......Xs gdzie N jest ilością powtórzeń pomiaru

w serii i powinna wynosić przynajmniej 10. Wartości rzeczywistej nie znamy. Ale z serii pomiarów wartością najbardziej zbliżoną do wartości rzeczywistej jest średnia arytmetyczna:

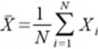
(3)

Jest to podstawowe twierdzenie teorii błędów tzw. pierwszy postulat Gaussa. Wynika on z faktu równości prawdopodobieństw tak zawyżenia wielkości mierzonej jak i jej zaniżenia. Tym samym błędy powinny kompensować się. Jednak przy skończonej ilości pomiarów, może się zdarzyć, że wyniki nie rozłożą się równomiernie wokół wartości rzeczywistej. Tym samym wartość średnia X jest jedynie blisko położona wielkości rzeczywistej Xr , ale nie równa jej. Zbliżenie to jest tym lepsze im dłuższa jest seria pomiarowa. Równość X=X_k moglibyśmy napisać tylko dla serii nieskończenie długiej pomiarów, ale przecież wykonanie takiej serii jest praktycznie niemożliwe. Wyniki pomiarów w serii rozkładają się wokół wartości średniej w tzw. krzywą Gaussa - mówi się o rozkładzie Gaussa. Aby się o tym przekonać należy zakres pomiarowy podzielić na przedziały o równej szerokości hX i obliczyć ile pomiarów z serii zmieściło się w każdym z nich (rys. 1).

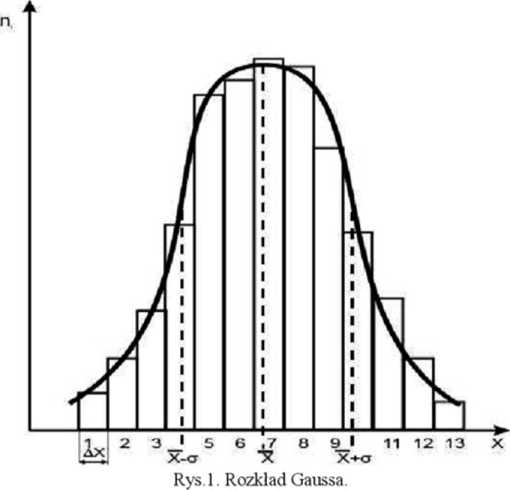
Oczywiście zwiększając N możemy pozwolić sobie na zmniejszenie szerokości poszczególnych schodków rozkładu, ale nadal zachowa on cliarakter dyskretny. Obwiednia dzwonowa poprowadzona po środkach schodków jak na rys. 1 jest pewnym wyidealizowaniem - pokazuje jak