98023

0

+ oo

Wartość rzeczywista

Prawostronny przedział ufności

\Lewostronny przedział ufności

—oo

kolejna próba losowa

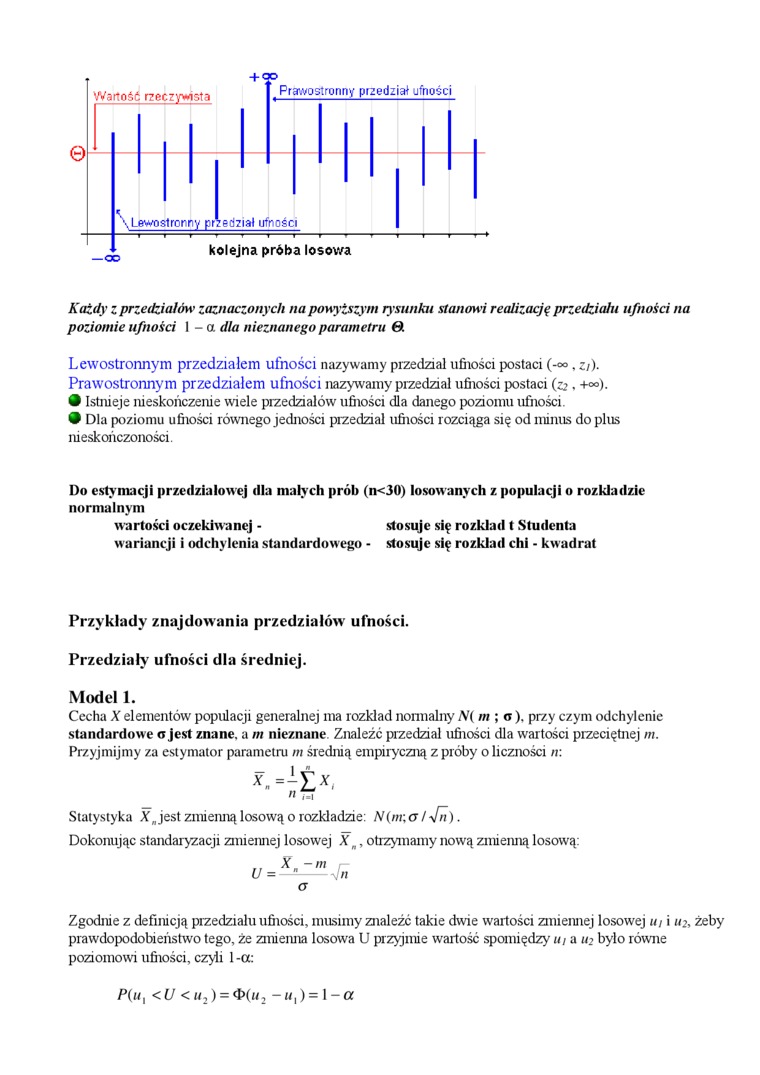
Każdy z przedziałów' zaznaczonych na powyższym ry sunku stanowi realizację przedziahi ufności na poziomie ufności I - o. dla nieznanego parametru O.

Lewostronnym przedziałem ufności nazywamy przedział ufności postaci (-«>, _Z/). Prawostronnym przedziałem ufności nazywamy przedział ufności postaci (z2. •*»).

® Istnieje nieskończenie wiele przedziałów ufności dla danego poziomu ufności.

• Dla poziomu ufności równego jedności przedział ufności rozciąga się od minus do plus nieskończoności.

I)o estymacji przedziałowej dla małych prób (n<30) losowanych z populacji o rozkładzie normalnym

wartości oczekiwanej -    stosuje się rozkład t Studenta

wariancji i odchylenia standardowego - stosuje się rozkład chi - kwadrat

Przykłady znajdowania przedziałów ufności.

Przedziały’ ufności dla średniej.

Model 1.

Cecha X elementów populacji generalnej ma rozkład normalny N( m ; o). przy czym odchylenie standardowe o jest znane, a m nieznane Znaleźć przedział ufności dla wartości przeciętnej m. Przyjmijmy za estymator parametru m średnią empiryczną z próby o liczności n:

1

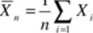
Statystyka X_n jest zmienną losową o rozkładzie: N{m\al4n).

Dokonując standaryzacji zmiennej losowej X _n, otrzymamy nową zmienną losową:

G

Zgodnie z definicją przedziału ufności, musimy znaleźć takie dwie wartości zmiennej losowej m i U2, żeby prawdopodobieństwo tego, że zmienna losowa U przyjmie wartość spomiędzy m a m? było równe poziomowi ufności, czyli 1-a:

P(u_x <U <m₂) = 4>(m₂ -u_l) = \-a