3784494692

Mamy dowieść, że

(i)

[.BCP]    CQ

[ADP] ~ DQ'

C

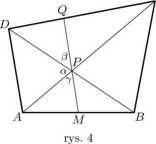
Wielkość CQ:DQ jest równa stosunkowi pól trójkątów CPQ i DPQ, gdyż oba trójkąty mają wspólną wysokość opuszczoną na podstawy CQ i DQ. Zatem równość (1) przybiera postać BP CP [CPQ]

AP DP ~ [DPQ]'

czyli

BPCP CPCQ-sin7 AP DP~ DP CQ-sin/?'

Należy więc dowieść, że

BP    sin 7

AP ~ sin p

lub BP-sm(3 = AP-sin7. Po pomnożeniu ostatniej równości przez \MP dowodzona przez nas tożsamość przybiera postać [BPM] = [APM]. Ta równość jest prawdziwa, gdyż punkt M jest środkiem boku AB. Dowód równości (1) jest więc zakończony.

Zadanie 7. Dana jest liczba naturalna n > 2. Wyznaczyć wszystkie wielomiany P(x) = ao + aix+...+a_nxⁿ mające dokładnie n pierwiastków nie większych niż —1 oraz spełniające warunek

<Zq + a\a_n = a^ + aoa_n-i.

Uwaga: Pierwiastki są liczone z uwzględnieniem krotności: jeśli liczba xo jest pierwiastkiem fc-krotnym wielomianu P(x) (tzn. jeśli wielomian P{x) jest podzielny przez wielomian (x — xo)^k, ale nie przez (x — xo)^k+1), wówczas liczba xq jest traktowana jak k pierwiastków wielomianu P(x).

Rozwiązanie

Niech — pi < —p2 < ... < —p_n będą pierwiastkami wielomianu spełniającego warunki zadania. Wówczas    oraz a_n ^ 0. Ponadto

a_n_i = a_n(pi+p₂ + ---+Pn), ai = a_npiP2-Pn(— + — + ... + — ).

^KP1    P2    Pn^J

oraz do = a_nPiP2---Pn■ Warunek Oq +aia_n =    + aoa_n_i można więc przepisać

w postaci

11 11

PlP2---Pn~\---1---K-d--—--\~Pl+P2 + ■■■ +Pn-

Pl P2    Pn    PlP2--Pn

Udowodnimy indukcyjnie, że dla n > 2 oraz dla dowolnych liczb rzeczywistych Pi ^ P2 ^    ^ Pn ^ 1 zachodzi nierówność

. . 11 11

(1) PlP2--Pn-\---1----->--\-Pl+P2 + ---+Pn

Pl P2    Pn PlP2-Pn

39