9990200032

2. Podstawy teoretyczne

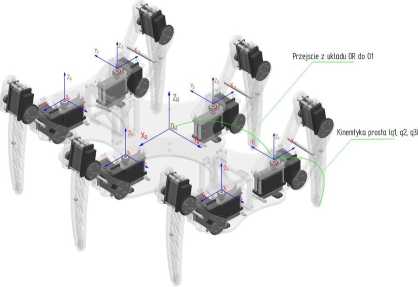
Rysunek 2.1 Rozmieszenie lokalnych układów współrzędnych, dla każdej z nóg

po obliczeniu uzyskuje się następujące macierze transformacji:

-1		0	0	-w
0		-1	0	h
0		0	1	0
. 0		0	0	1 .
1	0	0	w
0	1	0	k
0	0	1	0
p	0	0	1.

gdzie Zi i l₂ oznaczają pozycję lokalnego układu współrzędnych nogi względem układu Or. Wartości te można odczytać z rysunku 2.2. Na przykład dla nogi pierwszej (z — 1), h — ^au h — 0,3, natomiast dla i — 4, li = 01, l₂ — 03.

Do wyznaczenia kinematyki pojedynczej nogi (rysunek 2.3) posłużono się algorytmem Denavita-Hartenberga [18]. Przejście do kolejnych układów współrzędnych związanych z przegubami qi, q₂, <73 wygląda następująco:

?T = Rot (Z, _qi),

2T = Rot    ^ Trans (X, d\) Rot (Z, q₂),

\T — Trans (X, d₂) Rot (Z, 93),

\T = Trans {X, d₃).