3860644230

Asymptoty funkcji

Asymptota funkcji to prosta, do której przytula się wykres funkcji. Asymptota i wykres są bardzo blisko siebie w dużej odległości od początku układu.

Niektóre funkcje mogą przecinać swoje asymptoty lub pokrywać się z nimi.

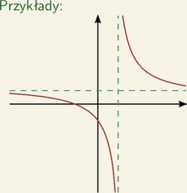
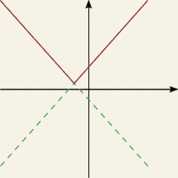
Asymptota pionowa

Funkcja f(x) ma asymptotę pionową w x = a, gdy lim f(x) = ±oo i lim /(x) = ±oo.

x—*a~    x—*a⁺

Przykłady:

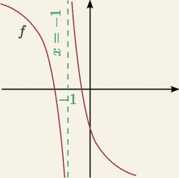
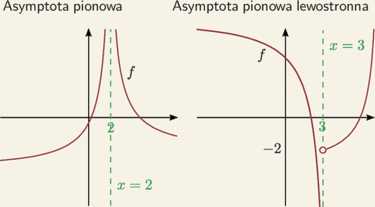
lim f(x) = oo

x—*2

lim /(x) = —oo

£—►3“

lim f(x) = -2

x^3+

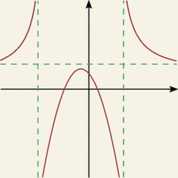
lim f(x) = —oo

X—► — 1”

lim f(x) = oo

X—* — 1 +

Asymptoty pionowe szukam licząc granice funkcji w punktach, które nie należą do dziedziny funkcji np. funkcja f(x) = -_x^_₄ ma dziedzinę IR \ {—2,2} czyli liczę \hn f(x) i

lim/(a;).

x—>2

Asymptota ukośna

f(x)

Funkcja f(x) ma asymptotę ukośną y = Ax + B, gdy lim - = A i

x—»±oo X

lim \f(x) — Ax\ = B.

x—*±oo

Przykłady:

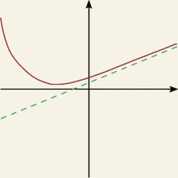
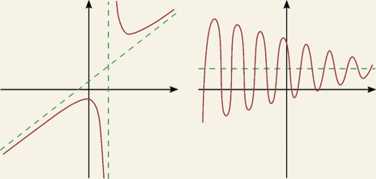
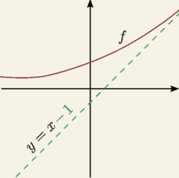
Asymptota ukośna    Asymptota ukośna w —oo    Asymptota ukośna w oo

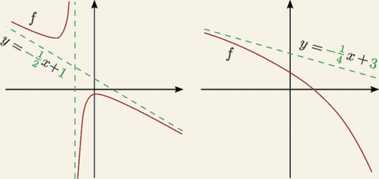
lim M

x—>—oc X

Hm M.-J x—*—oc X

hŁi

x—*oc x

lim [/(*)-(-i®)] = 1 lim \f(x) - ( - ^a:)] = 3 lim [f(x) - ls] = -1

lim

x—*oo x

lim [f(x) - ( - \x)\ = 1

Asymptota pozioma

/(*)

Asymptota pozioma to szczególny przypadek asymptoty ukośnej. Jeżeli lim - = O, to

£—►±00 x

funkcja f(x) ma asymptotę poziomą y = B, gdy lim f(x) = B.

x —► ±o©

Przykłady:

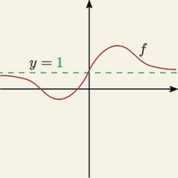
lim M _{= 0}

£—► — 00 X

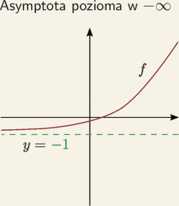
lim M ₌

£—► — 00 X

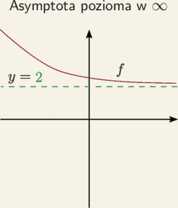
lim M,o

£—►00 X

lim f(x) = 2

lim f(x) = —1

lim f(x) = 1 £—►—00

lim M₌₀

£—►00 X

lim f(x) = 1

Zadania + Rozwiązania