5638685159

34 Układy arytmetyczne

dowywanc (dla słów o dowolnej długości) oraz, że ich przejrzysta struktura ułatwia testowanie. Wadą układów iteracyjnych jest to, że aby ustalił się wynik operacji, przeniesienie musi przejść przez wszystkie bloki, co powoduje zmniejszenie szybkości działania układu. Często, zwłaszcza w układach arytmetycznych. szybkość działania jest bardzo istotnym czynnikiem i dlatego poszukuje się takich struktur układów, które pozwolą na jej zwiększenie. Jednym z rozwiązań jest stosowanie układów przyspieszających.

W przypadku sumatorów wykorzystuje się układ obliczający przeniesienie grupowe dla pewnej grupy bitów, tzn. przeniesienie wyjściowe z najbardziej znaczącej pozycji grupy, wyznaczone na podstawie znajomości wartości wszystkich bitów obu słów wejściowych oraz bitu przeniesienia wejściowego.

Np. dla sumatora 4-bitowego przeniesienie grupowe będzie funkcją dziewięciu zmiennych: wejść danych a₃, aj, ai, ao, bj, bj, b/, bo i wejścia przeniesienia co. Jak pokazano wyżej funkcja przeniesienia z każdego bitu jest następująca: c_M-a, b + fatobje,.

Przyjmując oznaczenia: g, =o, b, i p,=a,® b, można otrzymać: ci^mgo+poCo

c( = gi+piC/= g, + pi go +p/ po co

cs^mgj+Pi cj = g2+ pj gi + pj p, g₀ + p₂ pi p₀ c₀

^c* ⁼ 8s⁺PiCj = g] + psg2⁺P3P:gi+pjp:p, go + p₃p:pi p₀ c₀

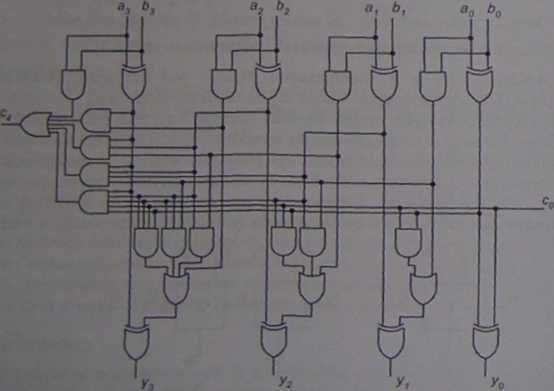
Ryt. 3.3. Sumator czterobitowv z układem generacji przeniesienia grupowego

Schemat sumatora 4-bitowego z układem przeniesienia grupowego jest pokazany na rys. 3.3. Łatwo sprawdzić, że sygnał z dowolnego wejścia do wyjścia przechodzi przez co najwyżej trzy bramki, znacznie mniej niż w przypadku odpowiedniego sumatora zbudowanego jako układ iteracyjny (sygnał z wejścia np. ao do wyjścia c< przechodzi przez 4x2 bramki). Oznacza to, że operacja sumowania liczb 4-bitowych jest realizowana blisko trzy razy szybciej przez sumator z przeniesieniem grupowym.

Symbol sumatora 4-bitowego jest pokazany na rys. 3.4. Układy takie można łączyć, budując sumatory słów o większej długości, tak jak pokazano na rys. 3.5 dla sumatora 16-bitowcgo. Układy takie, zbudowane z sumatorów realizujących przeniesienie grupowe, będą działały znacznie szybciej, niż zbudowane w postaci klasycznego układu iteracyjnego (z sumatorów jednobitowych).

i 1

A B

i

T3T

Rys. 3.4. Symbol sumatora czterobitowego

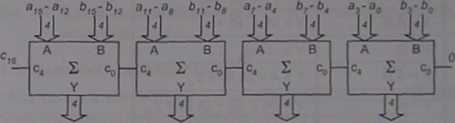
Rys. 3.5. Sumator 16-bitowy zbudowany z sumatorów 4-bitowych

3.4. Jednostka arytmctyczno-Iogiczna

Jednostka arytmetyczno-Iogiczna 1 ALU (ang. arithmetic and logie unit) jest kombinacyjnym blokiem funkcjonalnym umożliwiającym wykonywanie podstawowych operacji arytmetycznych i logicznych na liczbach (słowach) binarnych. Typowe operacje arytmetyczne realizowane przez ALU to dodawanie i odejmowanie, a także operacje jednoargumentowe: inkrementacja (dodanie 1), dekrementacja (odjęcie 1), mnożenie przez 2. Typowe operacje logiczne to suma, iloczyn, suma mod 2 (EXOR), negacja. Operacje logiczne są wykonywane osobno na każdej parze bitów. Na przykład:

0101    0101    0101

v OHO    a 0110    © 0110

om    óToo    ooiT

Przykładem ALU jest układ 74181 z serii układów TTL, którego symbol jest pokazany na rys. 3.6. Jest to układ 4-bitowy, który ma wejścia danych uj,...,oo i

bj.....bo, wejście przeniesienia co, wyjścia wyniku .v»,..._vv₀ i wyjście przeniesienia

^c4 oraz wejścia sterujące M, sj,...jo, których stan określa operację realizowaną