1673068231

13

FUNKCJE ANALITYCZNE

Dzięki i) widać, że definicja F nie zależy od wyboru 7. Dla odp. małych h mamy

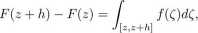
(4.3)

a stąd, dzięki (3.3), | F(z + h)~ F(z)

h

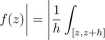
(/(C) -/(*))<£ S sup |/(() -/(z)|.

C G[z,z+h\

Z ciągłości / w 2 wynika, że ostatnie wyrażenie dąży do 0. Otrzymaliśmy zatem, że F G 0(fi) oraz F' = /.

Jeżeli fi jest gwiaździsty, to implikacja ii)^iii) jest trywialna, natomiast, zakładając, że zachodzi iii) i że fi jest gwiaździsty względem zq, kładziemy

j[z₀,z\

Iz, z € fi.

Z iii) wynika, że zachodzi (4.3) i identycznie jak poprzednio dowodzimy, że F' = /• □

Z Twierdzeń 4.1 i 4.2 wynika wersja twierdzenia Cauchy’ego dla zbiorów gwiaździstych.

Wniosek 4.3. Jeżeli obszar fi jest gwiaździsty i f € (9(D\{2o})nC(D) dla pewnego zq g fi, to f(z)dz = 0

7

dla każdej drogi zamkniętej 7 w £1.    □

5. Wzór całkowy Cauchy’ego

Podstawową własnością funkcji holomorficznych jest wzór całkowy Cauchy’ego (1831), który odtwarza daną funkcję wewnątrz koła z jej wartości na brzegu.

Twierdzenie 5.1. Jeżeli f jest funkcją holomorficzną w otoczeniu koła K(zo,r), to

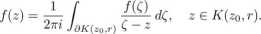
(5.1)

Co więcej, f jest C-różniczkowalna dowolną ilość razy oraz

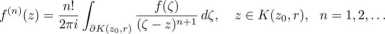
Dowód. Niech fi będzie gwiaździstym otoczeniem K(zq, r), w którym funkcja / jest określona. Dla £ € f2 zdefiniujmy

KO - KO